Контрольная работа: Застосування сплайн-функцій до розв’язування задач інтерполяції

Мал. 6, 7 – Розбіжності

Для цього будемо шукати максимальну похибку на кожному з відрізків розбиття. Скористаємося наступними формулами:

,(35)

Отже на проміжку маємо графік зображений на малюнку 8 (побудований в середовищі Mathcad). Неозброєним оком похибки не видно, але вона є, і це показано на малюнку 9, який зображає функцію .

Мал. 8 – Графік, побудований в середовищі Mathcad

Мал. 9 – Найбільша похибка відрізку

Як видно з малюнка 9, найбільша похибка на даному відрізку приблизно дорівнює:

при і відповідно .

Аналогічно розглянемо всі проміжки розбиття і знайдемо максимальні значення похибок на кожному з них, які представлені в наступній таблиці:

сегмент
	0,27	-2,023	0,021%
	0,82	-1,472	0,022%
	1,36	-0,584	0,028%
	1,78	0,584	0,028%
	2,34	1,489	0,021%
	2,88	2,023	0,021%

З таблиці видно, що максимальна похибка менша за 0,03%, і, оскільки, задовільною вважається похибка менша чим 5%, то отриману можна вважати практично нульовою.

3.2 Задача №2

Потрібно інтерполювати (використовуючи задачу першого або другого роду) одну з відомих функцій, з допомогою кубічних В-сплайнів, у випадку нерівномірної сітки розбиття.

Розв’язання: Для розв’язання цієї задачі візьмемо функцію і будемо її інтерполювати на відрізку , розбивши його на 5 частин ([0,1], [1,9/5], [9/5,12/5], [12/5,14/5], [14/5,3]). Маємо нерівномірну сітку, отже будемо користуватися формулою (15). Знайдемо і (задача інтерполяції першого роду). Аналогічно, як і в першій задачі використаємо формули (34) і розв’яжемо систему (33). Для нашої функції маємо наступні дані:

-2	-2
-1	-1
0	0	1	1
1	1
2
3
4
5	3
6	3,1
7	3,2

,,

,,

,,

,,

,,

,,

,,

,

,.

Тоді тридіагональна матриця і вектор відповідно дорівнюватимуть:

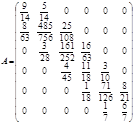,, підставивши

їх у матричне рівняння, отримаємо вектор :

,. Отже, маємо інтерполяційний сплайн функції на проміжку :

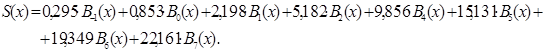
Побудуємо його графік (в середовищі Matlab):