Контрольная работа: Застосування сплайн-функцій до розв’язування задач інтерполяції

Мал. 2 - Графік В-сплайна

В-сплайн довільного степеня може бути відмінним від нуля лише на деякому відрізку (визначеному вузлами)[4].

2 Кубічні B -сплайни

2.1 Формули задання кубічних B-сплайнів

Зробивши аналогічні дії, що й при квадратичному В-сплайні, ми отримаємо формулу (15) для кубічного В-сплайна:

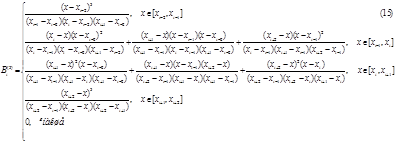
Зауваження. Кубічні В-сплайни зручніше нумерувати так, щоб сплайн був відмінний від нуля на відрізку [5]. Запишемо тепер у випадку рівномірної сітки (з кроком ) його:

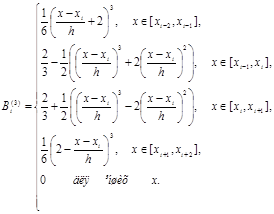(15’)

Типічний графік кубічного В-сплайну показано на мал. 3:

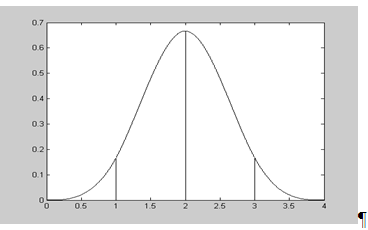
Мал. 3 - Типічний графік кубічного В-сплайну

2.2 Базис у просторі кубічних сплайнів

Функція :

а) двічі неперервно диференційовна на відрізку ;

б)відмінна від нуля тільки на чотирьох відрізках

Відрізок називають носієм функції [6].

Доповнимо розбиття допоміжними вузлами:

,взятими довільно.

За розширеною сіткою:

:можна побудувати сім’ю з кубічних В-сплайнів:

,

Ця сім’я утворює базис в просторі кубічних сплайнів на відрізку . Тим самим довільний кубічний сплайн , побудований по розбиттю із вузла, може бути представлений на цьому відрізку в вигляді лінійної комбінації:

Умовами задачі коефіцієнти цього розбиття визначаються однозначно [7].

2.3 Задачі інтерполяції з граничними умовами першого та другого роду

У випадку коли задані значення функції в вузлах сітки і значення і першої похідної функції на кінцях сітки (задача інтерполяції з граничними умовами першого роду), коефіцієнти обчислюються із системи наступного вигляду:

, де (16)

Після виключення і отримується лінійна система з невідомими і 3-діагональною матрицею, яку можна розв’язати, як методом Гауса, так і методом прогонки [8].