Курсовая работа: Анализ работы плоского рычажного механизма

Схема № 5

Вариант № 5

Положение механизма № 3

№	Параметры	Значение
1.	Частота вращения n, об/м	850
2.	lAB , мм	34
3.	lAС , мм	90
4.	lEF , мм	110
5.	lCD , мм	60
6.	lAE , мм	60
7.	Центры тяжести S1 , S2 ,S3 , S4 ,S5 расположены посередине соответствующих звеньев
8.	Расcтояние а, мм	40
9.	Расстояние b, мм	75
10.	Расcтояние c, мм	80
11.	Вес ползуна, Н	18
12.	Момент инерции звена	J = ml2 / 12
13.	Наибольшая сила сопротивления P, кH	300
14.	Масса звеньев m=ql, q=0.1 кг/м

1. ДИНАМИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА

1.1 СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМА

1.1.1 СТРУКТУРНАЯ СХЕМА МЕХАНИЗМА

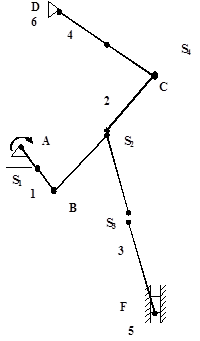
Рисунок 1.1. - Кинематическая схема механизма

Для изучения движения механизма необходимо знать его структуру: количество звеньев, количество и классы кинематических пар. Необходимыми также являются знания о взаимном расположении звеньев. Поэтому первым этапом кинематического анализа является построение кинематической схемы механизма. В данной курсовой работе рассмотрен механизм схемы № 5. Её построение выполнено в масштабе μ_l = 0,001 м .

Определить характер движения звеньев механизма можно с помощью плана положений. Построения плана начинается с черчения неподвижных опор B и D. Дальше строится траектория движения ведущего звена АВ (окружность) и на ней отмечаются двенадцать положений звена АС через каждые 30⁰ , начиная с того положения, которое соответствует самому верхнему положению ползуна, которое мы и принимаем за нулевое. По условию необходимо рассмотреть данный механизм в положении № 3. Кинематическая схема механизма приведена в заданном положении на рисунке 1.1.

1.1.2 ПЕРЕЧИСЛЕНИЕ ЗВЕНЬЕВ МЕХАНИЗМА

Рассмотрев характер движения, в механизме можно выделить следующие звенья:

1. - кривошип;

2. - шатун;

3. - коромысло;

4. - кривошип;

5. - ползун;

6. - стойка;

7. - стойка;

Звенья механизма соединены кинематическими парами:

1-2 - кинематическая пара 5-го класса, вращательная;

2-3 - кинематическая пара 5-го класса, вращательная;

2-4 - кинематическая пара 5-го класса, вращательная;

3-5 - кинематическая пара 5-го класса, вращательная;

6-1 - кинематическая пара 5-го класса, вращательная;

7-4 - кинематическая пара 5-го класса, вращательная;

3-5 - кинематическая пара 5-го класса, поступательная.

1.1.3 ОПРЕДЕЛЕНИЕ СТЕПЕНИ ПОДВИЖНОСТИ МЕХАНИЗМА

Разбиваем механизм на группы Ассура. Это показано на рисунке 1.2. Степень подвижности механизма определяем по уравнению Чебышева:

W = 3 n - 2 p ₅ - p ₄ (1.1.1),