Курсовая работа: Аналогія: теорема Піфагора на площині і в просторі

Але більш багатогранно аналогія виявляється у творчій діяльності людини. Велике значення має аналогія для творчого мислення.

Аналогія застосовується в учнівському пізнанні

П.М. Єрднієв вважає, що володіння ум овидом за аналогією «сприяє як творчості вченого – математика, так і успішному навчанню цієї науки або самостійному вивченню її».

Роль аналогії значно зростає в сучасних умовах навчання, коли перед школою стоїть завдання озброювати учнів не лише знаннями, а й методами самостійного здобуття знань.

Звернемо увагу на основні дидактичні функції аналогії. По-перше, аналогія сприяє більш глибокому осмисленню матеріалу, що вивчається. При цьому застосовується ті види аналогії, які конкретизують образи і уявлення. По-друге, аналогія при вивченні нового матеріалу допомагає підводити учнів до визначення нових для них понять, самостійних пошуків способу розв’язання задачі, ефективної організації повторення, узагальнення і систематизації матеріалу.

Вбачаючи в аналогії великі дидактичні можливості, вчені радять користуватись нею і вчителю, і учням. Проте слід пам’ятати, що висновки в умовиводах за аналогією не дає відповіді на питання про правильність припущення, ця правильність повинна перевірятись іншими засобами. Та аналогія важлива вже тим,що вона наводить на здогади, подає думку про те чи інше припущення. Це дуже важливо як у розвитку науки, так і в вивченні математики.

Звідси випливає актуальність вибраної теми.

Об'єкт дослідження – теорема Піфагора на площині і в просторі;

Предмет дослідження – аналогія між теоремою Піфагора на площині і в просторі;

Мета дослідження – розглянути в чому полягає аналогія міжтеоремою Піфагора на площині і в просторі.

Для реалізації поставленої мети необхідно розв'язати наступні завдання:

- підібрати, опрацювати та систематизувати літературні джерела з обраної теми;

- підібрати, класифікувати та зібрати задачі про теорему Піфагора на площині і в просторі (на доведення та обчислення).

Курсова робота складається зі вступу, двох розділів,висновку,списку використаної літератури, що містить 3 найменування.

У вступі визначається об'єкт, предмет,мета та завдання дослідження,обґрунтовується актуальність обраної теми,описана структура курсової роботи.

В наступних розділах йде огляд і доведення аналогії між трикутником та тетраедром.У висновку підведено підсумок про виконану роботу.

Розділ 1. Теорема Піфагора на площині

Теорема Піфагора . У прямокутному трикутнику квадрат довжини гіпотенузи дорівнює сумі квадратів довжини катетів.

Дано: ΔАВС, С = 90°, ВС = а, АС = b, АВ = с.

Довести : с² = а² + b²

1.1 Різні доведення теореми Піфагора

Доведення 1 . На гіпотенузі і катетах побудуємо квадрати і виконаємо додаткові побудови, які видно на рисунку 1. Тоді NAB = 90° + САВ,

САЕ =90° + САВ. Отже, NАВ = САЕ. Крім цього, NА = СА, АВ = АЕ.

Таким чином, за першою ознакою рівності трикутників маємо: ΔNAB = ΔCAE. Але S_ΔNAB = NA·NK = S_{ΔANRC ,} S_ΔCAE = AE·EH = S_AEHR . Порівнюючи останні три рівності, дістанемо: S_ANKC = S_{AEHR .} ( 1 ) Аналогічно, ABE = 90° + ABC, CBD = 90° + ABC. Звідси ABF = CBD. Крім того, AB – DB, CB – FB. Тоді за першою ознакою рівності трикутників ΔABF = ΔDBC. Але SΔABF = BF·QF = SBCQF, SΔDBC = BD·HD = SHRBD. З цих рівностей одержимо: SBCQA = SHRBD. ( 2 ) Додамо почленно рівності (1) і (2):

SANKC + SBCQF = SAEHR + SHRBD, але SAEHR + SHRBD = SAEDB.

Таким чином, SANKC+ SAEDBабо b2 + a2 = c2

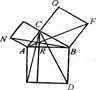
Рис. 1