Курсовая работа: Аналогія: теорема Піфагора на площині і в просторі

(Рис.2.1)

Доведемо, що

Маємо:

(1)

У Δ АВС:

, (2)

Площу трикутника АВС обчислимо за формою Герона

, де

Виконаємо перетворення:

,

.

Використовуючи (2), (3), одержимо:

тобто (4)

Враховуючи (1), (4), одержимо

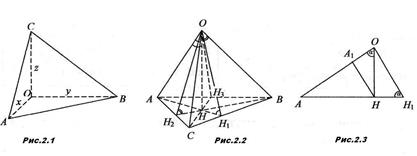
Розглянемо доведення, в якому використовується метод проекцій

Доведення 2

Нехай у прямокутному тетраедрі ОАВС грані ОВС, ОАС, ОАВ утворюють з основою АВС кути відповідно. Оскільки точка О проектується в ортоцентр Н трикутника АВС, то лінійні кути двогранних кутів при основі утворюватимуться висотами відповідних граней: (Рис. 2.2 ).Спроектуємо висоту ОН на ребра прямого тригранного кута, одержимо: ОА₁ =ОН (Рис. 2.3), аналогічно ОВ₁ =ОН, OC₁ =OH.

У прямокутному паралелепіпеді з діагоналлюОН і ребрами ОА₁ , ОВ₁ , ОС₁ справджується рівність

або ,

звідки (1)

Оскільки то ΔAOB – ортогональна проекція ΔАВС, аналогічно ΔAOC – ортогональна проекція ΔАВС і ΔBOС – ортогональна проекція ΔАВС.