Курсовая работа: Аналогія: теорема Піфагора на площині і в просторі

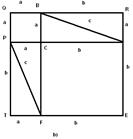
Рис.5,а

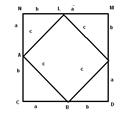
Рис.5,б

CDMN, TQRE – квадрати зі стороною . Тоді S_CDMN = S_TQRE .

За побудовою маємо:

S_CDMN = S_ABLK + 4S_ΔABC ,

S_TQRE = S_PQBC + S_ACFE + 4S_ΔABC .

Порівнюючи ці рівності, дістанемо:

S_ABLK + 4S_ΔABC = S_PQBC + S_ACFE + 4S_ΔABC , або

S_ABLK = S_PQBC + S_ACFE , тобто

Доведення 6

Побудуємо квадрат CDMN з стороною a+b( Рис.6)

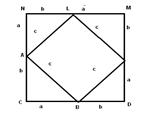
Рис. 6

Тоді ΔАСВ = ΔBDK = ΔKLM = ΔLNA ( за двома катетами ) , звідки

AB = BK = KL = LA = c.

Отже, чотирикутник ABKL – ромб.

Оскільки АВК = 90°, то ABKL – квадрат. Маємо:

Порівнюючи останні рівності, дістанемо:

Доведення 7

На сторонах прямокутного трикутника АВС побудуємо квадрати АВКМ, АDЕС, ВСFR. (Pис. 7). Трикутники ЕСF, КLМ і АСВ рівні між собою. АDRВ = EDRF як симетричні відносно прямої DR фігури; ACLM = КLСВ як центрально-симетричні фігури відносно центра квадрата АВКМ; АDRB=АСLМ як відповідні фігури при повороті навколо центра А на кут 90°.

Враховуючи одержані три рівності, маємо:

ADEFRB = ACBKLM, але

S_ADEFRB = S_ADEC + 2S_ΔABC + S_BCFR , S_ACBKLM = S_ABKM + 2S_ΔABC .

Отже, S_ADEC + S_BCFR = S_ABKM , тобто