Курсовая работа: Аналогія: теорема Піфагора на площині і в просторі

Доведення 2

Побудуємо ΔBDE = ΔACB так, щоб B CD ( рис 2).

Тоді чотирикутник ACDE – трапеція, бо AC || DE як два перпендикуляри до CD. Маємо:

S_ACDE = ·CD = ·² (1)

Крім того, S_ACDE = S_ΔABE + 2S_ΔABC . Трикутник ABE рівнобедрений і прямокутний. Дійсно, якщо позначимо АВС = BED = , тоді в прямокутному трикутнику BDEDBE = 90° - . За побудовою CBD = 90°.Таким чином, ABE = 180° - °, S_ΔABC =, S_ΔABC = .

Тоді S_ACDE = ( 2 )

Порівнюючи рівності ( 1 ) і ( 2 ), дістанемо:

Доведення 3. Побудуємо CDAB ( рис.3 ).

Нехай CAB = BCD = . Тоді S_ΔABC = sin. Оскільки ,

S_ΔABC = ( 1 )

Аналогічно: S_ΔACD = ( 2 )

S_ΔBCD = ( 3 )

За побудовою S_ΔABC = S_ΔACD + S_ΔBCD . ( 4 )

З рівностей ( 1 ), ( 2 ), ( 3 ), ( 4 ) випливає:

тобто

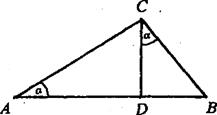Рис.3 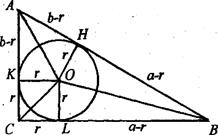Рис.4

Доведення 4. Впишемо в трикутник АВС коло ( О, r ) ( Рис.4 ). Тоді:

S_ΔABC = S_ΔOAC + S_ΔOAB =

Чотирикутник OKCL – квадрат з стороною r. За властивістю дотичних, проведених з точок А та В до кола, маємо: AH = AK = , BH = BL = .

Тоді

AB = AH + HB =

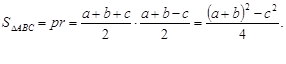
З іншого боку

S_ΔABC = .

Таким чином,

Доведення 5