Курсовая работа: Автоматическая система регулирования с П-регулятором

Получим систему двух линейных алгебраических уравнений первого порядка:

Найдем главный определитель матрицы:

Найдем вспомогательные определители системы:


Найдем коэффициенты а и b:

Таким образом, получим полином:
у =0.428 . х - 0.198
Для оценки полученного полинома вычислим значения функции и сравним их с экспериментальными данными.

Результаты вычисления сведем в таблицу. таблица 2
| i | x | y | yi | Δyi |
| 1 | 0 | 0 | -0.198 | 0.198 |
| 2 | 1 | 0.1 | 0.203 | -0.130 |
| 3 | 2 | 0.5 | 0.658 | -0.158 |
| 4 | 3 | 1 | 1.086 | -0.086 |
| 5 | 4 | 1.5 | 1.514 | -0.014 |
| 6 | 5 | 2 | 1.942 | 0.058 |
| 7 | 6 | 2.5 | 2.370 | 0.130 |
| 8 | 7 | 3 | 2.798 | 0.202 |
| 9 | 8 | 3.2 | 3.226 | -0.026 |
| 10 | 9 | 3.5 | 3.654 | -0.154 |
Сумма квадратов отклонений:
åDуi 2 = 0.174
Ниже приведен проверочный расчет модели объекта первого порядка на ЭВМ в системе MathCad.


1.3 Аппроксимация полиномом второго порядка
Модель второго порядка описывается уравнением вида:
у = а. х![]() + b. х + с.
+ b. х + с.
Для нахождения коэффициентов а, b, с, удовлетворяющих всем состояниям объекта регулирования составим систему алгебраических уравнений второго порядка, причем число уравнений в системе равно числу состояний объекта в эксперименте:
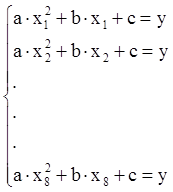
Для решения данной системы алгебраических уравнений воспользуемся матричным методом наименьших квадратов. Составим матрицы входных и выходных сигналов:
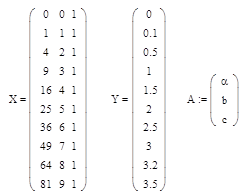
Получим систему с тремя неизвестными: X. A = Y
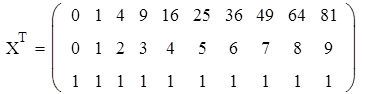 .
.
Решим матричное уравнение: