Курсовая работа: Автоматическая система регулирования с П-регулятором
Динамическая характеристика объекта регулирования
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | 0 | 0 | 0.5 | 0.71 | 0.8 | 0.91 | 0.98 | 0.99 | 0.995 | 1 |
Для получения аналитической зависимости, заданную таблично динамическую характеристику необходимо аппроксимировать экспоненциальным выражением первого порядка. Затем, по наименьшему значению суммы квадратов отклонений для характеристик без запаздывания и с запаздыванием, нужно выбрать наиболее приближенную к экспериментальным данным динамическую характеристику.
После расчета выполненного вручную следует проверить его на ПЭВМ в системе MathCad, а также произвести расчет динамической характеристики второго порядка и выбрать наиболее точную.
2.2 Модель объекта первого порядка без запаздывания
Динамическая модель первого порядка без запаздывания представляет собой неоднородное дифференциальное уравнение первого порядка:
(2.1)
где T - постоянная времени объекта;
k - коэффициент передачи при 50% номинального режима.
Решением уравнения (2.1) будет экспоненциальная зависимость сигнала на выходе от времени:
(2.2)
где y0 =0 - начальное состояние выхода объекта;
k. x=yуст. =10 - установившееся состояние выхода объекта.
Преобразовав выражение (2.2), получим:
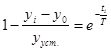(2.3)
Обозначим левую часть выражения (2.3) как 
. Значения и их натуральные логарифмы приведены в табл. 6.
Таблица 6
Значения и 
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| yi | 0 | 0 | 0.5 | 0.71 | 0.8 | 0.91 | 0.98 | 0.99 | 0.995 | 1 |
 | 1 | 1 | 0.5 | 0.29 | 0.2 | 0.09 | 0.02 | 0.01 | 0.005 | 0 |
 | 0 | 0 | -0.693 | -1.238 | -1.609 | -2.408 | -3.912 | -4.605 | -5.298 | -∞ |
Преобразовав выражение (2.3), получим:
откуда по методу наименьших квадратов найдем постоянную времени:
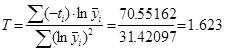
Таким образом динамическая характеристика первого порядка без запаздывания будет иметь вид:
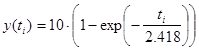
Вычислим аналитические значения функции, их отклонения от экспериментальных значений, а также квадраты отклонений и сведем их в
Таблица 7
Результаты расчета
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| yi | 0 | 0 | 0.5 | 0.71 | 0.8 | 0.91 | 0.98 | 0.99 | 0.995 | 1 |
| yi анал | 0 | 0.46 | 0.708 | 0.843 | 0.915 | 0.954 | 0.975 | 0.987 | 0.993 | 0.996 |
 yi | 0 | -0.46 | -0.208 | -0.133 | -0.115 | -0.044 | 4.8∙10-3 | 3.4∙10-3 | 2.2∙10-3 | 3.9∙10-3 |
 | 0.000 | 0.212 | 0.043 | 0.018 | 0.013 | 1.9∙10-3 | 2.3∙10-5 | 1.1∙10-5 | 4.9∙10-6 | 1.5∙10-5 |
Далее находим сумму квадратов отклонений:
Динамическая модель объекта первого порядка без запаздывания является наименее точной, поэтому ее применение не целесообразно при моделировании динамики объекта. Ниже приведен проверочный расчет динамической модели объекта первого порядка без запаздыванием и модели второго порядка без запаздыванием на ЭВМ в системе MathCad.