Курсовая работа: Автоматическая система регулирования с П-регулятором

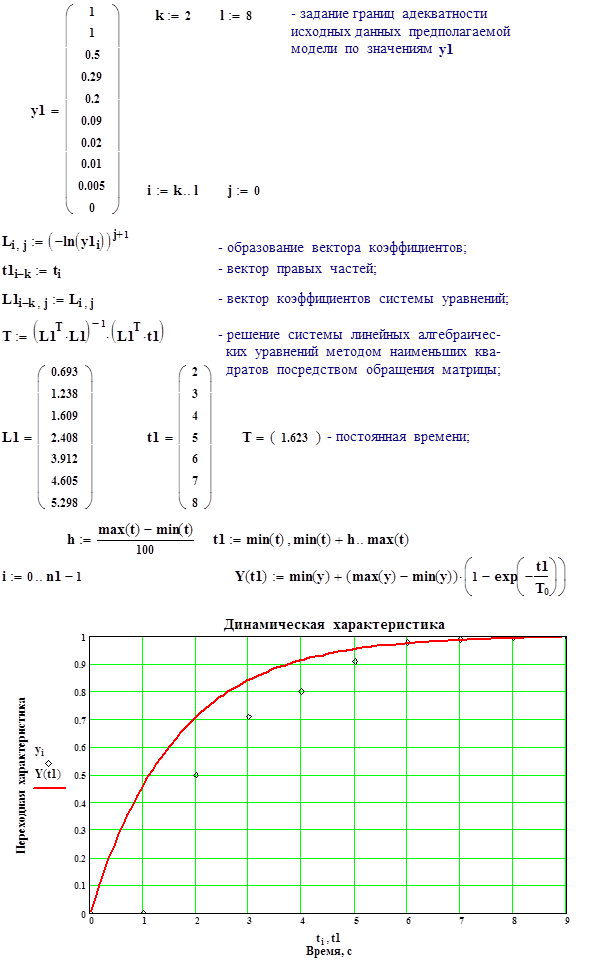
2.3 Модель объекта первого порядка с запаздыванием

Динамическая модель первого порядка с запаздыванием представляет собой неоднородное дифференциальное уравнение первого порядка:

(2.4)

где T - постоянная времени объекта;

k - коэффициент передачи при 50% номинального режима;

- время запаздывания.

Решением уравнения (2.1) будет экспоненциальная зависимость сигнала на выходе от времени:

(2.5)

где y₀ =0 - начальное состояние выхода объекта;

k^. x=y_уст. =10 - установившееся состояние выхода объекта.

Проведем преобразования, аналогичные модели без запаздывания

или запишем в виде системы :

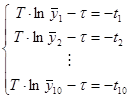(2.6)

где берется из табл. 7.

Так как , и , то все уравнения содержащие эти элементы в расчете участвовать не будут.

Решим систему (2.6) методом наименьших квадратов. Составим матрицы:

- искомых величин:

- правой части системы:

- левой части системы:

- произведение

- произведение

Таким образом получили матричное уравнение:

Находим главный определитель:

Подставляя матрицу поочередно в первый и второй столбец матрицы , находим вспомогательные определители: