Курсовая работа: Автоматическая система регулирования с П-регулятором

где А - матрица коэффициентов полинома второго порядка.

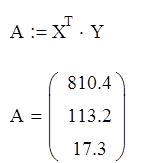
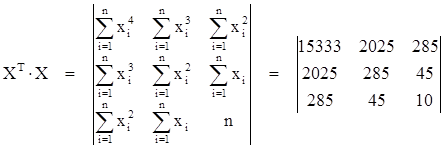Получим систему трех алгебраических уравнений

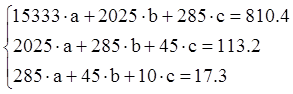
Решив ее, определим коэффициенты a, b, c.

Найдем главный определитель системы:

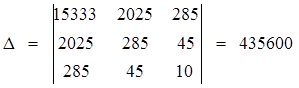
Найдем вспомогательные определители системы:

Найдем коэффициенты a,b,c:

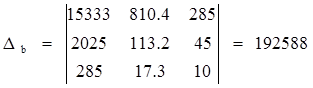
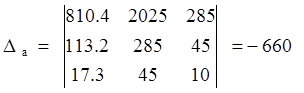
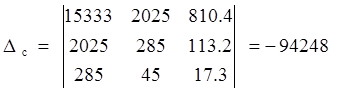
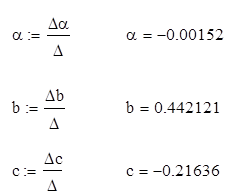
Таким образом, получили полином второго порядка:

y = -0.00152 ^. x_i ² + 0.442121 ^. x_i -0.21636

Для оценки полученного полинома вычислим значения функции и сравним их с экспериментальными данными:

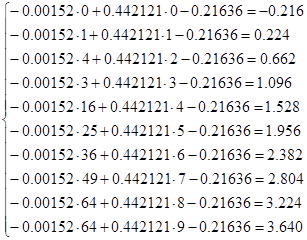
Полученные результаты сведем в таблицу 3

i	x	y	yi	Δy
1	0	0	-0.216	0.216
2	1	0.1	0.224	-0.124
3	2	0.5	0.662	-0.162
4	3	1	1.096	-0.096
5	4	1.5	1.528	-0.028
6	5	2	1.956	0.044
7	6	2.5	2.382	0.118
8	7	3	2.804	0.196
9	8	3.2	3.224	-0.024
10	9	3.5	3.640	-0.14

Сумма квадратов отклонений равна: åDу_i 2 = 0.173

Ниже приведен проверочный расчет модели объекта первого порядка на ЭВМ в системе MathCad.

Сравнивая суммы квадратов отклонений видно, что полином второго порядка лишь немногим точнее описывает поведение объекта, чем полином первого порядка. Из чего следует, что поведение объекта подчиняется уравнению очень близкому уравнению линии. Для расчетов используем уравнение найденное с помощью полинома второго порядка.

1.4 Расчет коэффициентов передачи

Для статической модели первого порядка коэффициент передачи определяется как производная от выходной величины:

Коэффициент передачи объекта показывает в какую сторону и в какой степени происходит изменение сигнала при прохождении его через объект, то есть усилительные свойства объекта.

Для статической модели первого порядка коэффициент передачи определяется как производная от выходной величины:

Для статической модели второго порядка коэффициент передачи определяется как производная от выходной величины:

Расчет коэффициентов передачи производим при 10, 50 и 90%