Курсовая работа: Численные методы интегрирования и оптимизации сложных систем

3.2.2 Метод Хука-Дживса

В данном методе поиск состоит из последовательности шагов исследующего поиска вокруг базисной точки, за которым, в случае успеха, проводится поиск по образцу.

Процедура поиска следующая.

Выбрать начальную базисную точку и шаг длиной для каждой из переменных , .

Вычислить в базисной точке с целью получения сведений о локальном поведении функции . Эти сведения будут использоваться для нахождения подходящего направления поиска по образцу, с помощью которого можно надеяться достичь большего убывания значения функции.

При поиске по образцу используется информация, полученная в процессе исследования, и минимизация функции завершается поиском в направлении, заданном образцом.

Завершить этот процесс, когда длина шага (длины шагов) будет уменьшаться до заданного малого значения.

3.3 Дифференциальное уравнение скорректированной системы

Для минимизации целевой функции (37) необходимо реализовать вычисление реального выходного сигнала в каждый отдельный момент времени. Помимо этого, необходимо реализовать итерационный процесс и реализовать алгоритм вычисления параметра

Для вычисления перейдём от передаточной функции замкнутой цепи к дифференциальному уравнению, используя свойства преобразований Лапласа. Оно будет иметь следующий вид:

(32)

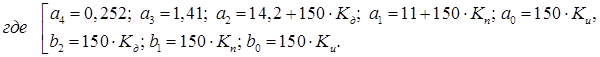
Запишем ДУ (32) в другом виде:

(33)

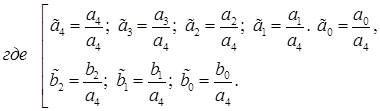
3.4 Нормальная форма Коши, полученного ДУ скорректированной системы

Для решения ДУ (33) с помощью численного метода решения дифференциальных уравнений, необходимо понизить его порядок, путём перехода от данного ДУ к нормальной форме Коши

Нормальная форма Коши для ДУ (33) будет иметь следующий вид:

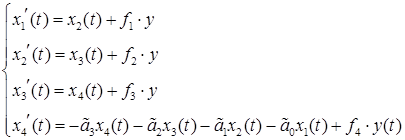
где коэффициенты рассчитываются по следующим формулам:

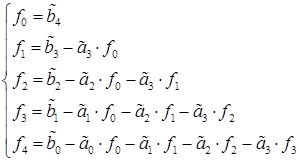
Тогда ДУ (33) можно записать в следующем виде

, (34)

где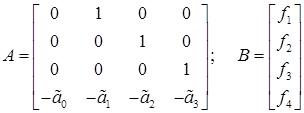

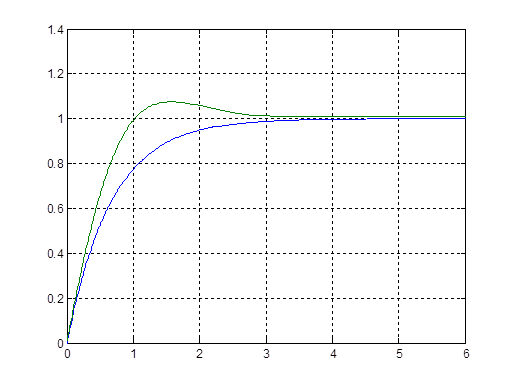
Рис. 13. Графики выходных сигналов скорректированной (зеленая линия) и нескорректированной (синяя линия) САУ.

Полученные параметры регулятора:

Кп=1.0547895

Кд=0.0550905