Курсовая работа: Численные методы интегрирования и оптимизации сложных систем

Рис.3. График движения корня в зависимости от номера итерации

2.3 Аналитические выражения для АЧХ, ФЧХ, АФЧХ

График АЧХ:

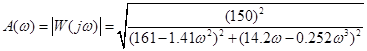
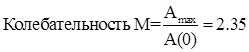
Функции, определяемые зависимостями (6) и (7), называются соответственно амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристиками.

Частотные характеристики определяются следующими показателями:

показатель колебательности - характеризует склонность системы к колебаниям: чем выше , тем менее качественна система (как правило в реальных системах );

резонансная частота - частота, при которой АЧХ имеет максимум (на этой частоте гармонические колебания имеют наибольшее усиление);

полоса пропускания системы – интервал от до , при котором выполняется условие ;

частота среза - частота, при которой АЧХ системы принимает значение, равное , т.е. ;

Частота среза косвенно характеризует длительность переходного процесса; справедливо соотношение 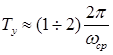. Таким образом можно сделать вывод: чем шире полоса пропускания, тем система является более быстродействующей.

2.4. Годограф АФЧХ и графики АЧХ и ФЧХ с указанием частот

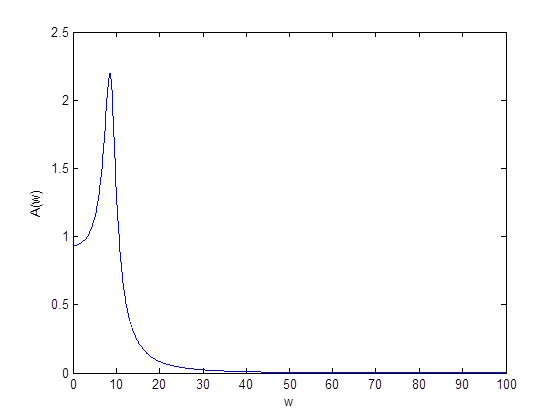
Рис.4 График АЧХ заданной САУ

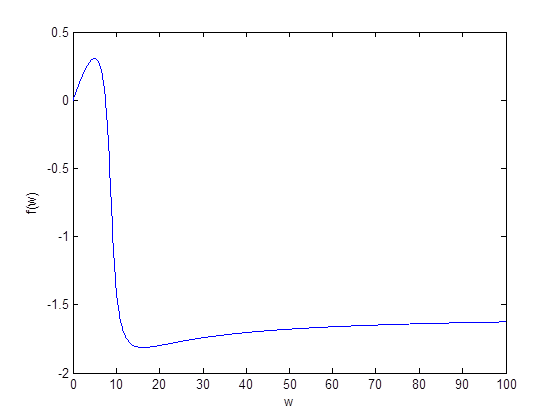
Рис.5 График ФЧХ заданной САУ

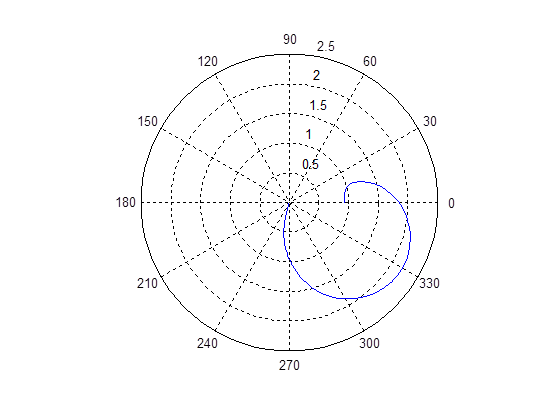
Рис.6 График АФЧХ заданной САУ

2.5 Дифференциальное уравнение заданной САУ

Получим ДУ заданной САУ:

2.6 Нормальная форма Коши, полученного ДУ 3-го порядка

Так как ДУ заданной САУ имеет высокий порядок, то его необходимо свести к системе уравнений, каждое из которых должно иметь первый порядок, т.е. имеет место нормальная форма Коши: