Курсовая работа: Численные методы интегрирования и оптимизации сложных систем

2.2.2 Метод секущих.

Проведём локализацию корней:

Построим график функции на интервале :

Рис.2. График характеристического полинома (3) на интервале

Уравнение имеет 1 действительный корень и 2 мнимых.

Уравнение решается методом секущих (4):

(4)

Возьмем начальное приближение и для нахождения действительного корня.

S=-8.210097

Далее получим значения комплексных корней:

Подставим в (5)

Получаем корни характеристического уравнения:

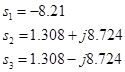
Вывод: 2 полюса передаточной функции находятся в правой полуплоскости. Система неустойчива.

2.2.3 Движение действительного корня полинома в s-плоскости

Построим график движения корня в зависимости от номера итерации: