Курсовая работа: Численные методы интегрирования и оптимизации сложных систем

Так как ДУ заданной САУ имеет укороченную правую часть, то запишем нормальную форму Коши в следующем виде:

. (10)

Приведём уравнение (12) к нормальной форме Коши:

(11)

или

,

где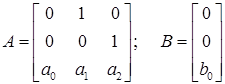

2.7 Аналитическое решение ДУ

Пусть задано изображение выхода

или .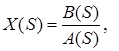

Тогда используя вторую теорему разложения Лапласа 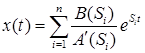получим следующее аналитическое выражение для выходного сигнала:

реакция системы на единичное ступенчатое воздействие () (12):

(12)

2.8 Решение ДУ численным методом(метод Рунге-Кутта 5-го порядка и метод Адамса неявный 4-го порядка)

В неявных методах используется информация о возможном будущем значении решения в точке п+1. Это несколько повышает точность получаемых результатов по сравнению с явными методами.

Для организации вычислительного процесса по интерполяционной формуле Адамса, имеющей точность решения (13):

необходимо заготовить начальные значения , используя метод Рунге-Кутта 5-его порядка.

Приведенные коэффициенты:

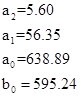
Проведём исследование решения ДУ в зависимости от шага:

Графики выходного сигнала, полученного в аналитическом виде , выходного сигнала, полученного решением ДУ и ошибки решения при шаге h=0.1 и h=0.01, h=0.001.

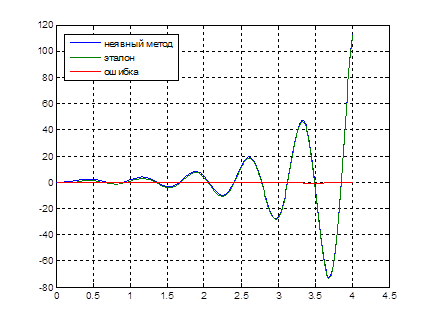
Рис.7. Графики выходного сигнала , полученного в аналитическом виде, выходного сигнала , полученного численным решением ДУ и ошибки решения при шаге

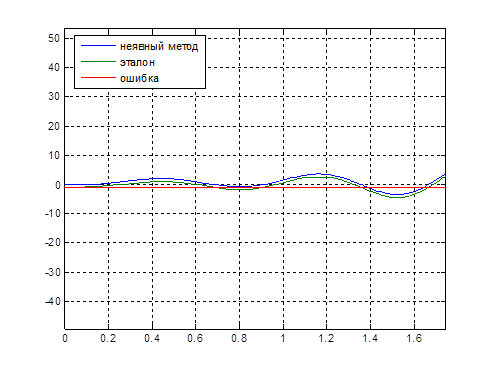
Рис.8. Графики выходного сигнала , полученного в аналитическом виде, выходного сигнала , полученного численным решением ДУ и ошибки решения при шаге