Курсовая работа: Численные методы интегрирования и оптимизации сложных систем

(25)

Передаточная функция замкнутой системы будет иметь вид (26):

(26)

Для решения задачи синтеза необходимо найти параметра регулятора , структура которого заданна (формула 31), при которых реальный выходной сигнал , являющийся реакцией на единичное ступенчатое воздействие, будет близок к заданному эталонному сигналу .

В качестве эталонного выходного сигнала выберем следующий сигнал:

, (27)

где параметр находится по следующей зависимости:

. (28)

3.2 Функционал качества, подлежащий дальнейшей минимизации

Критерием близости выберем метрику пространства .

Тогда целевая функция, подлежащая минимизации по параметрам регулятора будет иметь следующий вид:

(29)

3.2.1 Поиск минимума функции методом Фибоначчи

Если начальный интервал имеет длину , то произведя вычислений функции, можно уменьшить начальный интервал неопределённости в раз по следующей формуле:

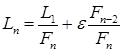(30)

по сравнению с его начальной длинной (пренебрегая ).

Если определить последовательность чисел Фибоначчи следующим образом: для то можно найти положение первой точки, которая помещена на расстоянии от одного из концов начального интервала, причём не важно, от какого конца, поскольку вторая точка помещается согласно правилу симметрии на расстоянии от конца интервала:

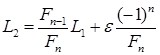. (31)

После того, как найдено положение первой точки, числа Фибоначчи больше не нужны. Используемое значение может определятся из практических соображений. Оно должно быть меньше , иначе будут иметь место лишние вычисления значений функции .

Таким образом, поиск методом Фибоначчи является итерационной процедурой.

В процессе поиска интервала с точкой , уже лежащей в этом интервале, следующая точка всегда выбирается такой, что .

Обозначим и , тогда можно рассмотреть четыре случая организации вычислительного процесса:

1. : новый интервал .

2. : новый интервал .

3. : новый интервал .

4. : новый интервал .