Курсовая работа: Дифференциальное уравнение относительного движения механической системы

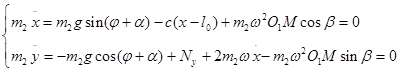(1.1.2)

. Выберем φ₀ =0 → φ=;

Рассмотрим проекцию на ось Ох. Разделим обе части уравнения на массу тела:

, где (1.1.3)

Общее решение полученного линейного неоднородного дифференциального уравнения с постоянными коэффициентами будем искать виде

x=X+,

где Х – общее решение соответствующего однородного уравнения,

-частное решение неоднородного уравнения.

Однородное уравнение имеет вид

=0, (1.1.4)

которому соответствует следующее характеристическое уравнение

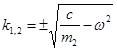i,

Т.к. величина под корнем отрицательна, то общим решением однородного дифференциального уравнения (1.1.3) будет являться функция:

Х=,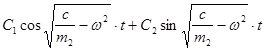

где С₁ и С₂ – постоянные интегрирования.

Частное решение уравнения (1.1.3) будем находить как результат суперпозиции двух решений: .

Для имеем:

(1.1.5)

, где k=0, значит

Подставим в (1.1.4):

При sin: