Курсовая работа: Дифференциальное уравнение относительного движения механической системы
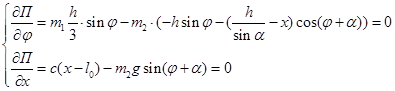
Решая систему уравнений, получаем два возможных положение равновесия:
.
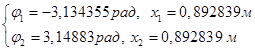Для оценки устойчивости полученных положений равновесия определим обобщенные коэффициенты жесткости. Найдем все вторые производные потенциальной энергии (3.1) по обобщенным координатам:
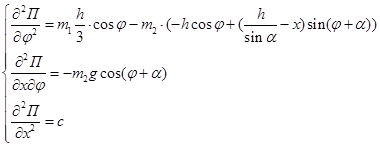
Для первого положения равновесия обобщенные коэффициенты жесткости равны:
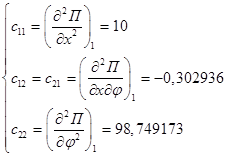
Воспользуемся критерием Сильвестра:
Для второго положения равновесия обобщенные коэффициенты жесткости равны:
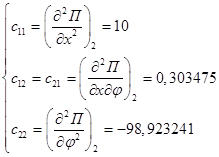
Воспользуемся критерием Сильвестра:
Таким образом, система принимает единственное устойчивое положение равновесия при: 
3.2 Частоты главных колебаний. Уравнения движения материальной точки и твердого тела при колебаниях
Для нахождения частот и форм главных колебаний, выпишем полученные значения обобщенных коэффициентов инерции и жесткости в положении устойчивого равновесия, при: .
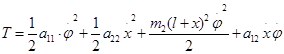
В положении равновесия:
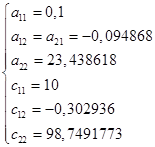(3.2.1)
Запишем дифференциальные уравнения малых колебаний механической системы:
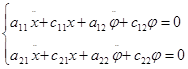
Составим характеристическое уравнение:
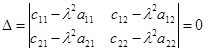
Или в развернутом виде:
Найдем корни характеристического уравнения, подставляя в уравнение найденные значения обобщенных коэффициентов инерции и жесткости: