Определим коэффициенты форм колебаний:

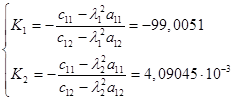
Таким образом, движение рассматриваемой системы при собственных колебаниях будет происходить по следующему закону:

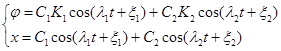(3.2.2)

3.3Уравнения движения материальной точки и твердого тела при колебаниях

Найдем значения постоянных интегрирования системы уравнений (3.2.2) для следующих начальных условий:

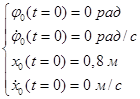
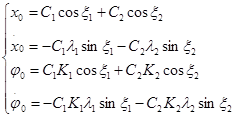
Решая систему уравнений, получим:

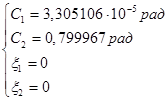
С учетом полученных значений постоянных интегрирования запишем окончательный вид уравнений колебаний:

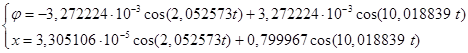
Список использованной литературы

1. Авраменко А.А., Архипов В.В., Асланов В.С., Тимбай И.А. Динамика точки и механической системы. – Самара: СГАУ. – 2001. – 84 с.

2. СТП СГАУ 6.1.4. – 97. Общие требования к оформлению учебных текстовых документов: методические указания.