Курсовая работа: Дифференциальные уравнения
Московский авиационный институт
(государственный технический университет)
Филиал "Восход"
Кафедра МиПОИС
Курсовая работа
по курсу: Дифференциальные уравнения
Студент гр. ДА 2-40
Воронцов О. В.
Байконур 2005 г.
1. Теоретическая часть
Дифференциальные уравнения, приводящиеся к однородным
Дифференциальные уравнения, которые приводятся к однородным, имеют вид:
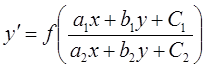
Возможны три случая:
1) Когда C1 =C2 =0
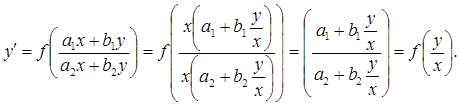
2) Когда
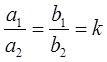
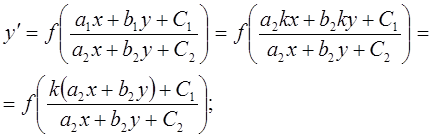
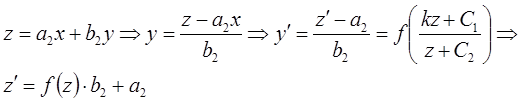
Когда
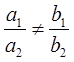
Вводятся новые переменные u и υ так, чтобы правая часть исходного уравнения в этих переменных была однородной функцией нулевого порядка. А именно, делается замена x=u+h, y= υ+k и подбираются постоянные h и k таким образом, чтобы в правой части исходного уравнения после подстановки пропали свободные члены. При подстановке x=u+h, y= υ+k в дробь приравниваются нулю свободные члены числителя и знаменателя, то есть записываются два равенства:
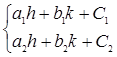
Определитель данной системы линейных алгебраических уравнений: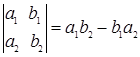 
, не равен нулю по условию, поэтому система имеет единственное решение, то есть существует единственная пара чисел h и k, такая что при подстановке x=u+h, y= υ+k правая часть исходного уравнения принимает вид 
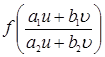, а само уравнение: 
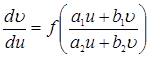. Полученное уравнение является однородным
2. Практическая часть
Задача 1. Найти общий интеграл дифференциального уравнения:
Решение:
– дифференциальное уравнение с разделяющимися переменными
Разделим переменные:
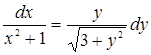
Проинтегрируем выражение:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--