Курсовая работа: Дифференциальные уравнения

Откуда:

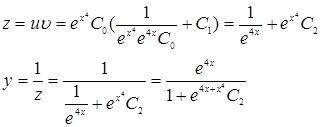
Найдём значение С₂

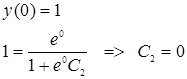
Следовательно:

Ответ:

Задача 7. Найти общий интеграл дифференциального уравнения:

Решение:

- дифференциальное уравнение в полных дифференциалах

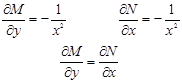
Следовательно, левая часть уравнения является полным дифференциалом некоторой функции

(*)

Интегрируем по x первое из уравнений (*), при этом считаем, что С является функцией от y:

Дифференцируя полученное, имеем:

Но

Откуда:

Следовательно:

Ответ:

Задача 8. Для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через точку М.