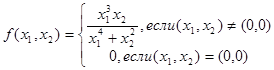(11)

Эта функция непрерывна всюду на плоскости, включая точку (0,0). В точке (0,0) ее слабый дифференциал существует и равен 0, поскольку

Вместе с тем этот дифференциал не является главной линейной частью приращения функции (11) в точке (0,0). Действительно, если положить h₂ =h₁ ² , то

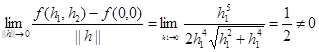
Однако если отображение Fимеет сильную производную, то оно имеет и слабую, причем сильная и слабая производные совпадают. Действительно, для сильно дифференцируемого отображения имеем

А(ч + ер) — А (ч) = Аэ (ч) (ер) + о (ер) = еАэ (ч)р +о (ер) и

Выясним условия, при которых из слабой дифференцируемости отображения Fследует его сильная дифференцируемость.

Теорема 1. Если слабая производная F'_c (х) отображения Fсуществует в некоторой окрестности Uточки х₀ и представляет собой в этой окрестности (операторную) функцию от х, непрерывную в x₀ , то в точке x₀ сильная производная F'(x₀ ) существует и совпадает со слабой.

Доказательство. По е>0 найдем д>0 так, чтобы при ||h||< д бвыполнялось неравенство:

|| F'_c (x_o + h)-F'_c (x_o ) || е

Применив к отображению Fформулу (10), получим:

|| F(x₀ + h)-F(х_о ) - F'_c (х_о ) h|| ||F'_c (x_o + иh)- F'_c (x_o )||

||h|| е||h||

Тем самым имеет место теорема 1, т. е. доказано как существование сильной производной F'(x_о ), так и ее совпадение со слабой производной.

Дифференцируемые функционалы

Мы ввели дифференциал отображения F,действующего из одного нормированного пространства X в другое нормированное пространство У. Производная F'(х) такого отображения при каждом х — это линейный оператор из X в У, т. е. элемент пространства о(X, У). В частности, если У — числовая прямая, то F— принимающая числовые значения функция на X, т. е. функционал. При этом производная функционала Fв точке х₀ есть линейный функционал (зависящий от х₀ ), т. е. элемент пространства X*.

Пример. Рассмотрим в действительном гильбертовом пространстве Н функционал F(x)= ||х||² . Тогда

||x+ h||² -||x||² = 2(x, h) + || h||² ;

величина 2(x,h)представляет собой главную линейную (по h) часть этого выражения, следовательно,

F' (x) = F'_c (x) = 2х.

Абстрактные функции

Предположим теперь, что к числовой прямой сводится пространство аргументов X. Отображение F(x),сопоставляющее числу х элемент некоторого банахова пространства У, называется абстрактной функцией. Производная F'(х) абстрактной функции (если она существует) представляет собой (при каждом х) элемент пространства У — касательный вектор к кривой F(x).Для абстрактной функции (представляющей собой функцию одного числового аргумента) слабая дифференцируемость совпадает с сильной.

Интеграл

Пусть F— абстрактная функция действительного аргумента tсо значениями в банаховом пространстве У. Если Fзадана на отрезке [а, b], то можно определить интеграл функции Fпо отрезку [а,b]. Этот интеграл понимается как предел интегральных сумм

,

отвечающих разбиениям

ф = е₀ Бе₁ Б ююю Бе_т = иб о_л хе_л бе_л+1 ъб

при условии, что max(t_{k +1} -t_k ) 0. Интеграл (представляющий, собой, очевидно, элемент из Y) обозначается символом

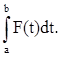
Рассуждения, в значительной мере аналогичные проводимым для функций, принимающих скалярные значения, показывают, что интеграл от функции, непрерывной на отрезке, существует; при этом он обладает свойствами обычного риманова интеграла.

Производные высших порядков