||R_n ||

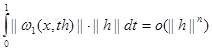
Тем самым наше утверждение доказано.

Формулу (21) называют формулой Тейлора для отображений.

Заключение

В этой работе представлены некоторые первоначальные понятия , относящиеся к нелинейному функциональному анализу, в основном к теории дифференцирования, и некоторые применения этих понятий.

Некоторые задачи, возникающие в функциональном анализе, носят существенно нелинейный характер; они приводят к необходимости развивать наряду с «линейными» и « нелинейными» функциональный анализ, т.е изучать нелинейные функционалы и нелинейные операторы в бесконечномерных пространствах.

К нелинейному функциональному анализу относится, по существу, такая классическая область математики, как вариационное исчисление, основы которого были заложены еще в XVII-XVIIIвв. в работах Бернулли, Эйлера, Лагранжа. Однако в целом нелинейный функциональный анализ представляет собой сравнительно новую область математики, пока еще далекую от своего завершения.

Список литературы:

1. Колмогоров А.Н., Фомин С.В. - Элементы теории функций и функционального анализа. М., Наука, 1981. – 475 с.

2. Шилов Г.Е. – Дифференцирование функций в линейном пространстве. Ярославль, 1978. – 118стр.

3. Банах С. – Дифференциальное и интегральное исчисление. М.,Наука, 1972. – 424стр.