Курсовая работа: Дослідження кривої й форми поверхні другого порядку

,

зі зменшенням , центр еліпса (0;0;h)

При різних h маємо:

Якщо , тоді й значить лінії задовольняючому рівнянню(1) немає.

2. Розглянемо отримані в перетинах еліпсоїда площинами X=h:

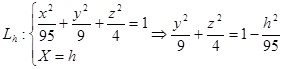(2)

Рівняння проекцій на YOZ.

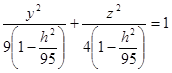
Це рівняння еліпсів з півосями

,

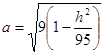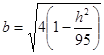
Якщо , то a=3, b=2, і

Якщо , тоді ми одержуємо сімейство еліпсів:

, ;

, ;

Якщо , тоді — це рівняння крапки з координатами (h;0;0).

Якщо , тоді й значить лінії задовольняючому рівнянню (2) немає.

3. Розглянемо отримані в перетинах еліпсоїда площинами Y=h:

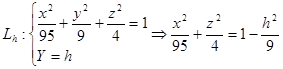(3)

Рівняння еліпсів, проекцій на YOZ і мають центри (0;h;0).

Півосі ,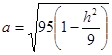

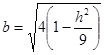
Якщо , тоді , рівняння крапок з координатами (0;h;0).

Якщо , тоді ми одержуємо сімейство еліпсів

, ;

, ;

Якщо , тоді й значить лінії задовольняючому рівнянню (3) немає.

Побудуємо гіперболоїд