Висновок

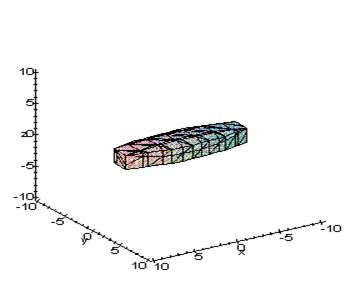
Проаналізувавши рівняння еліпсоїда

одержали деякі подання про форму еліпсоїда.

З рівняння треба, що осі OX, OY, OZ - осі симетрії, площини XOY, YOZ, XOZ - площини симетрії.

Розсікаючи поверхню площинами y=h, z=h, x=h, у перетинах маємо еліпси, найбільші з яких виходять у площинах x=0, y=0, z=0, півосі їх зменшуються зі збільшенням , вершини еліпсів мають координати

по осі X; по осі Y; по осі Z

Список літератури

1. Копилова Т. В. Конспект лекцій по лінійній алгебрі. – К., 2005

2. Копилова Т. В. Лінійна алгебра. – К., 1996

3. Єфімова Л. В., Демидович Б. П. Лінійна алгебра й основи математичного аналізу. – К., 1993.