Множачи обидві частини рівності (1) на й використовуючи подання через , як і раніше, одержимо:

. (13)

Знову вийшла система лінійних алгебраїчних рівнянь із трикутною матрицею для визначення . Трохи ускладнивши обчислення можна одержати систему діагонального виду. Для цього побудуємо три системи векторів , так що мають місце рівності:

(14)

(15)

(16)

Тоді

, (17)

тому що при i<r

(18)

і при i>r

(19)

Таким чином,

(20)

Зупинимося докладніше на першому з описаних методів. Розглянемо випадок, коли матриця А симетрична й позитивно певна. Останнє означає, що для будь-якого вектора квадратична форма його компонент більше або дорівнює нулю, причому рівність нулю можливо в тім і тільки тім випадку, якщо вектор нульової. Як ми бачили раніше, потрібно побудувати систему векторів , що задовольняють умовам

=0 . (21)

Це побудова можна здійснити в такий спосіб. Виходимо з якоїсь системи лінійно незалежних векторів , наприклад із системи одиничних векторів, спрямованих по координатних осях:

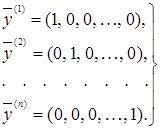(22)

Далі проводимо «ортогоналізацію». Приймаємо й шукаємо у вигляді

. (23)

З умови знаходимо:

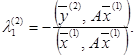(24)

Шукаємо у вигляді

. (25)

Умови спричиняють

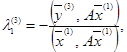
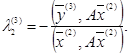(26)

Далі надходимо також.

Процес буде здійсненний, тому що все . Це ж забезпечить нам можливість розв'язання системи для визначення коефіцієнтів . Помітимо, що в нашім випадку це буде процес справжньої ортогоналізації, якщо в просторі векторів увести новий скалярний добуток за допомогою співвідношення

. (26)

Неважко перевірити, що уведене таким способом скалярний добуток буде задовольняти всім вимогам, які до нього пред'являються.