Курсовая работа: Дослідження методу ортогоналізації й методу сполучених градієнтів

Будемо шукати мінімум функціонала (2) на множині векторів

. (26)

Дорівнюючи до нуля частки похідні від по й для визначення й , одержимо систему:

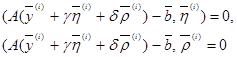(27)

або, з огляду на (25),

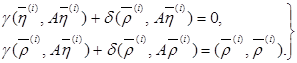(28)

Позначимо через рішення цієї системи:

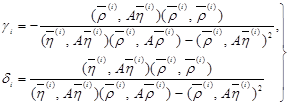(29)

і за (i+1) – е наближення до рішення приймемо:

(30)

Із системи (27) треба, що

, (31)

а тому що

те з (31) треба:

(32)

Доведемо, що якщо

(33)

те при всіх i

(34)

що буде доводити й збіжність, і кінцівка другого алгоритму.

Справді, при умовах (33)

т.ч. умова (24) виконано. Припустимо, що вже доведено рівності

(35)

і доведемо рівність

При припущенні (35) і, отже,