Курсовая работа: Дослідження методу ортогоналізації й методу сполучених градієнтів
Але зі співвідношень (20) маємо:
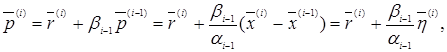
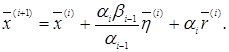
Доведемо коллінеарність векторів
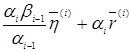 і
і ![]() (36)
(36)
З (20) і (29) маємо:
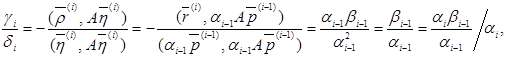
а це й доводить коллінеарність векторів (36).
Вектор ![]() дає мінімум функціонала в площині, що проходить через
дає мінімум функціонала в площині, що проходить через ![]() і на вектори
і на вектори ![]() й
й ![]() , а ми показали, що цей мінімум лежить на прямій, що проходить через
, а ми показали, що цей мінімум лежить на прямій, що проходить через ![]() у напрямку вектора
у напрямку вектора ![]() . Але на цієї прямий мінімум функціонала досягається на векторі
. Але на цієї прямий мінімум функціонала досягається на векторі ![]() . Це й означає, що
. Це й означає, що ![]()
Це й доводить справедливість (34) при всіх i.
На перший погляд здається, що перший алгоритм краще, тому що на кожному кроці він вимагає лише одного множення матриці А на вектор ![]() , а в другому алгоритмі потрібно два множення матриці А на вектор
, а в другому алгоритмі потрібно два множення матриці А на вектор ![]() і
і ![]() , але досвід показав, що застосування першого алгоритму приводить до швидкого нагромадження помилок округлення, так що для матриць великого порядку можливо істотне відхилення від точного рішення. Другий алгоритм менш чутливий до помилок округлення й тому вимагає меншого кількість кроків для одержання гарного наближеного рішення.
, але досвід показав, що застосування першого алгоритму приводить до швидкого нагромадження помилок округлення, так що для матриць великого порядку можливо істотне відхилення від точного рішення. Другий алгоритм менш чутливий до помилок округлення й тому вимагає меншого кількість кроків для одержання гарного наближеного рішення.
Метод сполучених градієнтів доцільно використовувати для рішення систем рівнянь, у яких матриця А має багато нульових елементів. При рішенні системи по цьому методі елементи матриці беруть участь в арифметичних операціях лише при множенні матриці на вектор, а множення матриці на вектор можна організувати так, щоб в арифметичних операціях брали участь тільки ненульові елементи.
Висновок
У даній роботі були розглянуті метод ортогоналізації й метод сполучених градієнтів, а також представлена програма мовою програмування С++, що реалізує метод ортогоналізації на ЕОМ, і її результати роботи.
Список літератури
1. Березин І.С. і Жидков Н.П. Методи обчислень. – К., 2003
2. Воєводін В.В. Чисельні методи алгебри (теорія й алгоритми). – К., 2004
3. Подбельський В.В. і Фомін С.С. Програмування мовою С ++. – К., 2002
4. Каліткін М.М. Чисельні методи. – К., 2003