Курсовая работа: Дослідження методу ортогоналізації й методу сполучених градієнтів
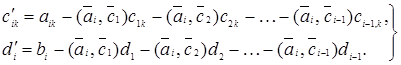(40)
Процес буде здійсненний, якщо система рівнянь лінійно незалежна. У результаті ми прийдемо до нової системи 
, де матриця З буде ортогональної, тобто має властивість СС¢=I.
Таким чином, рішення системи можна записати у вигляді
. (41)
Практично, внаслідок помилок округлення, СС¢ буде відмінна від одиничної матриці й може виявитися доцільним зробити кілька ітерацій для системи 
.
2. Метод сполучених градієнтів
2.1 Перший алгоритм методу
Нехай потрібно вирішити систему лінійних алгебраїчних рівнянь
(1)
с позитивно певною матрицею A порядку n.
Розглянемо функціонала
, (2)
багаточлен, що представляє, другого порядку відносно x 1, x 2…, xn ,… Позначимо через 
рішення системи (1), тобто 
. У силу симетричності й позитивної визначеності матриці, маємо:
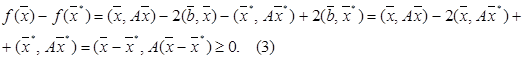
При цьому знак рівності можливий лише при 
. Таким чином, задача рішення рівняння (1) зводиться до задачі відшукання вектора 
, що обертає в мінімум функціонал (2).
Для відшукання такого вектора застосуємо наступний метод.
Нехай 
– довільний початковий вектор, а
(4)
– вектор не в'язань системи. Покажемо, що вектор не в'язань 
має напрямок нормалі до поверхні 
в крапці 
. Справді, напрямок нормалі збігається з напрямком найшвидшої зміни функції 
в крапці . Це напрямок ми знайдемо, якщо знайдемо серед векторів 
, для яких 
, такий вектор, що
має найбільше значення. Але
Але серед векторів постійний довжини 
досягає максимального значення, якщо має напрямок вектора або йому протилежне. Твердження доведене. Будемо рухатися із крапки в напрямку вектора доти, поки функція 
досягає мінімального значення. Це буде при 
, тобто при
. (5)
Вектор
(6)
і приймаємо за нове наближення до рішення.
У методі сполучених градієнтів наступне наближення 
перебуває так. Через крапку 
проведемо гіперплощину (n-1) – го виміру
(7)