Курсовая работа: Дослідження методу ортогоналізації й методу сполучених градієнтів

(16)

буде мати напрямок нормалі до перетину поверхні гіперплощиною (14) у крапці . Із крапки змістимося в напрямку цього вектора так, щоб функція досягла мінімального значення. Це буде при

, (17)

(18)

приймемо за нове наближення к. Новий вектор не в'язань буде:

. (19)

Продовжуючи процес, одержимо послідовності векторів , , , обумовлені рекурентними співвідношеннями:

(20)

Для цих векторів мають місце наступні співвідношення:

(21)

(22)

Справді, у силу самої побудови при i (j

Далі, при i>j

Якщо i=j+1, то права частина дорівнює нулю, у силу визначення , якщо ж i>j+1, те, по доведеному, і

.

Продовжуючи зниження індексу у вектора , через кілька кроків прийдемо до скалярного добутку (по визначенню ). Таким чином, співвідношення (21) доведені. Для доказу (22), у силу рівноправності індексів i і j, припустимо, що i>j. Тоді

.

Тому що в n-мірному векторному простори не може бути більше n взаємно ортогональних векторів, то на деякому кроці одержимо , тобто буде рішенням системи (1).

На мал. 1 показана геометрична картина нашої побудови при n=3.

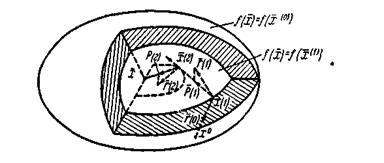
Мал. 1

2.2 Другий алгоритм методу

Приведемо інший алгоритм методу. Будемо позначати послідовні наближення до рішення через і введемо позначення:

. (23)

Перші два наближення й візьмемо так, щоб

. (24)

Припустимо, що вже відомо наближення (i³1), обчислена й справедливо рівність