Курсовая работа: Дослідження методу ортогоналізації й методу сполучених градієнтів

(28)

операцій множення й ділення.

1.2 Метод ортогоналізації у випадку несиметричної матриці

У випадку несиметричної матриці процес ортогоналізації проводиться точно також. Нехай вектори вже побудовані. Тоді шукається у вигляді

(29)

Коефіцієнти визначаються із системи

(30)

Система у випадку несиметричної матриці буде трикутною.

Аналогічно будується система «біортогональних» векторів, тобто система 2n векторів, що задовольняють умові (12). При цьому – n довільних лінійно незалежних векторів, а вектори будуються послідовно у вигляді

(31)

Коефіцієнти перебувають із системи

(32)

Також надходимо, відшукуючи коефіцієнти й , при побудові систем векторів (14) і (15), що задовольняють умовам (16).

При цьому одержимо дві системи:

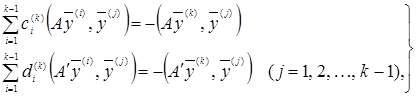(33)

з яких і визначаємо й .

Зупинимося ще на одному методі ортогоналізації. Будемо розглядати рядки матриці А як вектори:

(34)

Перше рівняння системи ділимо на 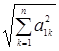. При цьому одержимо

(35)

де

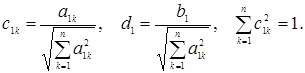(36)

Друге рівняння системи заміниться на

(37)

де

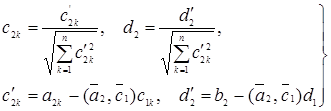(38)

Аналогічно надходимо далі. Рівняння з номером i прийме вид

(39)

де