Курсовая работа: Економічні задачі лінійного програмування і методи їх вирішення
Z=x1 +2x2 ¦mах
Система обмежень:
3 x1 +3 x2 <= 15 2 x1 +6 x2 <= 18 4 x1 <= 16 x1 +2x2 <= 8 Xj>=0, j=1..2
Зведення задачі до канонічного виду: Zmax = x1 +2x2 при умовах:
3x1 +3x2 +x3 = 15 2x1 +6x2 +x4 = 18 4x1 +x5 = 16 x1 +2x2 +x6 = 8 Xj>=0, j=1..6
Таблиця 5.
| Базис | С | План | 1 | 2 | 0 | 0 | 0 | 0 |
| X3 | 0 | 15 | 3 | 3 | 1 | 0 | 0 | 0 |
| X4 | 0 | 18 | 2 | 6 | 0 | 1 | 0 | 0 |
| X5 | 0 | 16 | 4 | 0 | 0 | 0 | 1 | 0 |
| X6 | 0 | 8 | 1 | 2 | 0 | 0 | 0 | 1 |
| Zj-Cj | 0 | -1 | -2 | 0 | 0 | 0 | 0 |
Таблиця 6.
| Базис | С | План | 1 | 2 | 0 | 0 | 0 | 0 |
| X3 | 0 | 6 | 2 | 0 | 1 | -0,5 | 0 | 0 |
| X2 | 2 | 3 | 40238 | 1 | 0 | 40330 | 0 | 0 |
| X5 | 0 | 16 | 4 | 0 | 0 | 0 | 1 | 0 |
| X6 | 0 | 2 | 40238 | 0 | 0 | -0,3333 | 0 | 1 |
| Zj-Cj | 6 | -0,3333 | 0 | 0 | 40238 | 0 | 0 |
Таблиця 7.
| Базис | С | План | 1 | 2 | 0 | 0 | 0 | 0 |
| X1 | 1 | 3 | 1 | 0 | 40210 | -0,25 | 0 | 0 |
| X2 | 2 | 2 | 0 | 1 | -0,1667 | 40269 | 0 | 0 |
| X5 | 0 | 4 | 0 | 0 | -2 | 1 | 1 | 0 |
| X6 | 0 | 1 | 0 | 0 | -0,1667 | -0,25 | 0 | 1 |
| Zj-Cj | 7 | 0 | 0 | 40330 | 40269 | 0 | 0 |
Відповідь: Zmax =7, Xопт =(3 ; 2 ; 0 ; 0 ; 4 ; 1).
Це свідчить про те, що максимальний прибуток підприємства буде дорівнювати 7 грн., а виробництво продукції А і В складає відповідно 3 і 2 одиниці.
3.2 Вирішення задачі лінійного програмування за допомогою «Пошуку рішень» у середовищі Microsoft Office Excel 2003
«Пошук рішень» – одна із сервісних можливостей пакету Microsoft Office Excel 2003. Він представляє собою спрощений варіант симплекс-методу.
«Пошук рішень» викликається за допомогою меню «Сервіс», далі вибираємо підменю «Надстройки» і натискаємо «Пошук рішень» [12].
Методика знаходження рішення задачі за допомогою «Пошуку рішень» в Excel полягає в тому, що користувач задає основні параметри завдання (цільову функцію, систему обмежень) і змінні клітинки, яким дають деякі довільні початкові значення (одиниці). Після цього «Пошук рішень» автоматично перебирає всі можливі значення змінюваних клітинок так, щоб вони задовольняли обмеженням, а цільова функція приймала задані значення. Таким чином, порядок виконання «Пошуку рішень» такий [3]:
1. На аркуші Excel формується масив, відповідний розширеній матриці системи обмежень задачі (блок клітинок В2:С5 та Е2:Е5).
2. Виділяються клітинки, відповідні змінним завдання, яким присвоюються початкові значення, які дорівнюють одиницям (В8:С8).
3. Виділяється клітинка, в якій обчислюється значення цільової функції, яка містить посилання на клітинки змінних (у клітинку В10 вводимо формулу =1*B8+2*C8).
4. Створюється масив, відповідний лівим і правим частинам системи обмежень. Для цього з посиланням на клітинки коефіцієнтів і змінних обчислюються складові лівих частин системи обмежень, і обчислюється сума (у клітинку В12 вводимо формулу =B2*B8, у клітинку В13 вводимо =B3*$B$8 і далі тягнемо мишкою вниз ще на дві клітинки; у клітинку С12 вводимо =C2*$C$8 і тягнемо вниз; відповідно у клітинках Е12-Е15 обчислимо суму построково). Це все проілюстровано на рисунку 1.
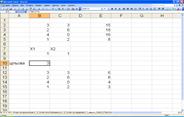
Рис. 1.
5. Після запуску «Пошуку рішень» задається адреса цільової клітинки, спрямованість цільової функції, адреса змінюваних клітинок, система обмежень, умова невід’ємності значень змінних. Вікно «Пошуку рішень» зображено на рисунку 2.
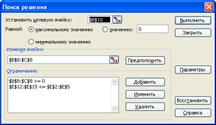
Рис. 2.
6. У параметрах виділяється лінійна і невід'ємна моделі. Дивись рисунок 3.
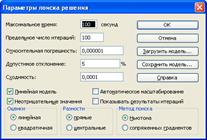
Рис. 3.
7. Проводиться запуск. У випадку, якщо необхідне рішення знайдено, воно зберігається. Це вікно зображене на рисунку 4.
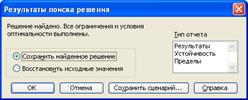
Рис. 4.