Курсовая работа: Економічні задачі лінійного програмування і методи їх вирішення

. (9)

Оскільки x_i (θ) при θ = 0 визначають план задачі, то найбільше θ, яке не порушує обмеження x_i (θ) ≥ 0, визначається із умови

. (10)

де I = {i | x_ik > 0}.

В силу невиродженості задачі мінімум досягається не більш ніж для одного i = J та θ > 0. Значення лінійної форми при θ = θ₀ визначається із рівнянь (9), (4), (2)

,

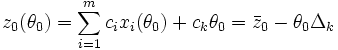де Δ_k = z_k — c_k . Очевидно, Δ_j = 0 для j = 1, …, m.

Нехай — початковий базис із m одиничних векторів. Всі дані задачі записуються у вигляді симплекс-таблиці (першої ітерації обчислювального процесу). Симплекс-алгоритм розв'язання задачі лінійного програмування складається із наступних операцій:

1. знайти Δ_k = min_j Δ_j . Якщо Δ_k = 0, тоді план, який розглядається оптимізовано; якщо Δ_k < 0, вектор A_k вводиться в базис;

2. знайти θ₀ та l, для якого , із формули (10). Якщо I = Λ — порожня множина, лінійна форма необмежена зверху; якщо I ≠ Λ вектор A_l виводиться із базису;

3. за знайденими l, k обчислити нові значення елементів таблиці за формулами

4.

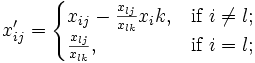(12)

,

де та перейти до виконання операції (1) з новими значеннями всіх x_ij = x'_ij .

Перетворення (12) замінює вектор коефіцієнтів X_k = (x_1k , …, x_mk ) на одиничний вектор X_k з x_lk = 1. В силу монотонного збільшення x₀ повернення до вже пройденого плану неможливе, а із скінченності кількості опорних планів випливає скінченність алгоритму.

Початковий опорний план з одиничним базисом можна отримати, розв'язавши описаним алгоритмом допоміжну задачу

,

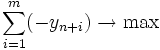при обмеженнях

;

,

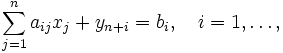
яка містить одиничний базис, який складається із векторів A_n+1 , …, A_n+m . Цим векторам відповідають штучні змінні із значеннями , i = 1, …, m. Якщо в оптимальному розв'язку цієї задачі 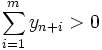, вихідна задача не має розв'язку. Якщо ж 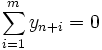та задача невироджена, оптимальний базис складається лише тільки із векторів вихідної задачі, які за формулами (12) перетворені в одиничну матрицю. Якщо задача має невироджені плани, значення z₀ може не збільшуватись на ряді ітерацій. Це відбувається через те, що значення відповідних дорівнює нулю та визначається неоднозначно. В таких випадках монотонність методу порушується і може трапитись зациклювання, тобто, повернення до вже пройденого базису. Невелика зміна вектора обмежень задачі, яка полягає в заміні величин b_i на b_i + ε_i , де ε_i достатньо малі, при вдалому виборі ε_i не змінюють множину векторів оптимального опорного плану вихідної задачі і робить її невиродженою.

Описаний вище алгоритм називається першим (або прямим) алгоритмом симплекс-методу. Також відомий другий алгоритм (алгоритм із оберненою матрицею). В ньому перетворюється лише матриця A^-1 , обернена до базисної матриці.

3. Прикладний розділ

3.1 Вирішення задачі лінійного програмування симплекс-методом

Для розробки математичної моделі задачі позначимо:

x₁ – кількість продукту А;

x₂ – кількість продукту В;