Курсовая работа: Економічні задачі лінійного програмування і методи їх вирішення

1.2 ПРИКЛАДИ ЕКОНОМІЧНИХ ЗАДАЧ лінійного програмування

1.2.1 Задача оптимального виробничого планування

Для виготовлення n видів продукції P1, ..., Pn використовується m видів сировини S1, ..., Sm, запаси якого обмежені і становлять відповідно b1, ..., bm одиниць. Відомо, що на виробництво одиниці продукції Pj (j =) витрачається аij одиниць ресурсу Si (i =, а прибуток від реалізації одиниці продукції Pj (j=) становить сj (j =.)

Потрібно визначити план виробництва, який дозволяє при готівкових ресурсах отримати максимальний прибуток підприємства від реалізації продукції [15].

Перш за все, запишемо умови задачі компактно у вигляді таблиці:

Таблиця 1.

Вид продукції Вид сировини	Р1	...	Pj	...	Pn	Запас ресурсу
S1	a11	...	a1j	...	a1n	b1
...	...	...	...	...	...	...
Si	ai1	...	aij	...	ain	bi
...	...	...	...	...	...	...
Sm	am1	...	amj	...	amn	bm
Прибуток	c1	…	cj	…	cn

Складемо математичну модель задачі.

Позначимо через xj (j =) плановане до випуску кількість продукції Рj (j=), а через Z (х1, ..., xn) – прибуток підприємства від реалізації всієї продукції. Тоді планом виробництва буде вектор Х = (х1, ..., хn), що показує, яку кількість продукції кожного виду буде вироблено. Змінні х1, ..., хn – керовані змінні. Мета рішення задачі (критерій оптимальності) – максимізувати прибуток:

Z = c1x1 + c2x2 +. . . + cnxn .

Сумарні витрати ресурсу Si (i = складають:

.

У силу обмеженості ресурсу Si величиною bi отримаємо систему обмежень:

.

На змінні хj повинна бути накладена умова невід’ємності

тобто продукція Рj або може випускатися (xj > 0), або не випускатися (xj = 0).

Отже, математична модель буде мати вид:

,

.

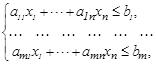
1.2.2 Задача про суміші

Задача визначення оптимального складу суміші виникає тоді, коли з наявних видів сировини шляхом їх змішування необхідно отримати кінцевий продукт із заданими властивостями. До цієї групи завдань відносяться, наприклад, завдання отримання сумішей для різних марок бензину в нафтопереробній промисловості, сумішей для отримання бетону в будівництві, завдання про вибір дієти, складання кормового раціону в тваринництві та інше. При цьому потрібно, щоб вартість такої суміші була мінімальною.

Нехай є m видів сировини, запаси якого становлять відповідно d1, ..., dm. З цієї сировини необхідно скласти суміш, яка містить n речовин, що визначають технічні характеристики суміші. Відомі величини визначають -кількість j-ї речовини в одиниці-го виду сировини, ціна якого дорівнює а також найменший допустимий кількість j-ї речовини в суміші.

Потрібно забрати суміш із заданими властивостями при найменших витратах на вихідні сировинні матеріали.

Для складання математичної моделі запишемо умови задачі у вигляді таблиці: