Курсовая работа: Економічні задачі лінійного програмування і методи їх вирішення
Вид речовини
Вид сировини
Обсяг сировини
Ціна
сировини
Мінімальна кількість речовини в суміші
b1
...
bj
...
bn
Позначимо через хi 
кількість сировини і-го виду, що входить у склад суміші.
Мета завдання (цільова функція) – мінімізувати сумарні витрати на сировину:
Система обмежень включає в себе обмеження за технічними характеристиками:
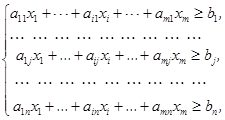
а також обмеження за обсягом сировини, які з урахуванням невід’ємності будуть мати вид:
Запишемо модель у компактній формі:
при обмеженнях:
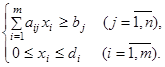
1.2.3 Задача про розкрій
Задача оптимального розкрою матеріалів полягає у визначенні найбільш раціонального способу розкрою наявного матеріалу (колоди, сталеві смуги, шкіра і т.д.), при якому буде виготовлено найбільшу кількість готових виробів у заданому асортименті чи буде досягнуто найменшу кількість відходів. Нехай на обробку поступає a одиниць сировинного матеріалу одного виду (наприклад, a колод однієї довжини). З нього потрібно виготовити комплекти, в кожен з яких входить n видів виробів у кількості, пропорційній числах. Є m способів розкрою (обробки) даного матеріалу, тобто відомі величини визначають кількість одиниць j-х виробів при i-му способі розкрою одиниці сировинного матеріалу [10].
Визначити план розкрою, що забезпечує максимальну кількість комплектів. Згідно з умовами завдання маємо таблицю розкрою:
Таблиця 3.
|
Вид виробу Спосіб розкрою |
К-во Просмотров: 428
Бесплатно скачать Курсовая работа: Економічні задачі лінійного програмування і методи їх вирішення
|