Курсовая работа: Економічні задачі лінійного програмування і методи їх вирішення

для яких цільова функція досягає максимуму.

Компактна форма моделі має вид:

,

,

. [9].

2.2 Симплекс-метод

Симплекс-метод — метод розв'язання задачі лінійного програмування, в якому здійснюється скерований рух по опорних планах до знаходження оптимального розв'язку; симплекс-метод також називають методом поступового покращення плану [6].

Опишемо метод.

Нехай невироджену задачу лінійного програмування представлено в канонічному вигляді:

,

де X = (x₁ , …, x_n ) — вектор змінних,

C = (c₁ , …., c_n ), B = (b₁ , …, b_m )^T ,

A_j = (a_1j , …, a_mj )^T , j = 1, …, n — задані вектори,

T — знак транспонування, та

відмінні від нуля компоненти опорного плану, для полегшення пояснення розташовані на перших m місцях вектору X. Базис цього плану — . Тоді

, (1)

, (2)

де значення лінійної форми на даному плані. Так як вектор-стовпці матриці A лінійно незалежні, будь який із векторів умов A_j розкладається по них єдиним чином:

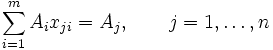, (3)

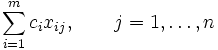, (4)

де x_ij коефіцієнт розкладання. Система умов

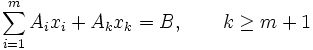, (5)

z_k ≥ 0, x_j = 0, j = m + 1, …, n, j ≠ k (6)

при заданому k визначає в просторі змінних задачі промінь, який виходить із точки, яка відповідає опорному плану, що розглядається. Нехай значення змінної x_k при русі по цьому променю дорівнює θ, тоді значення базисних змінних дорівнюють x_i (θ). В цих позначеннях рівняння (5) можна представити в виді

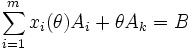. (7)

помноживши рівняння (3) на θ при j = k та віднявши від рівняння (1), отримаємо

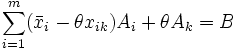. (8)