Курсовая работа: Функции Бесселя

2) теплопроводность в цилиндрических объектах;

3) формы колебания тонкой круглой мембраны;

4) скорость частиц в цилиндре, заполненном жидкостью и вращающемся вокруг своей оси.

Функции Бесселя применяются и в решении других задач, например, при обработке сигналов.

Цилиндрические функции Бесселя являются самыми распространенными из всех специальных функций. Они имеют многочисленные приложения во всех естественных и технических науках (особенно в астрономии, механике и физике). В ряде задач математической физики встречаются цилиндрические функции, в которых аргумент или индекс (иногда и тот и другой) принимают комплексные значения. Для численного решения таких задач необходимо разработать алгоритмы, позволяющие вычислять функции Бесселя с высокой точностью.

Цель курсовой работы: изучение функций Бесселя и применение их свойств в решении дифференциальных уравнений.

Задачи:

1) Изучить уравнение Бесселя и модифицированное уравнение Бесселя.

2) Рассмотреть основные свойства функций Бесселя, асимптотические представления.

3) Решить дифференциальное уравнение с использованием функции Бесселя.

1 Функции Бесселя с целым положительным значком

Для рассмотрения многих проблем, связанных с применением цилиндрических функций, достаточно ограничиться изучением специального класса этих функций, который соответствует случаю, когда параметр в уравнении (1) равен нулю или целому положительному числу.

Исследование данного класса носит более элементарный характер, чем теория, относящаяся к произвольным значениям , и может служить хорошим введением в эту общую теорию.

Покажем, что одним из решений уравнения

0, 1, 2, …, (1.1)

является функция Бесселя первого рода порядка , которая для любых значений определяется как сумма ряда

(1.2)

При помощи признака Даламбера легко убедиться, что рассматриваемый ряд сходится на всей плоскости комплексного переменного и, следовательно, представляет целую функцию от .

Если обозначить левую часть уравнения (1.1) через и ввести сокращенную запись коэффициентов ряда (1.2), положив

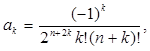
то в результате подстановки получим

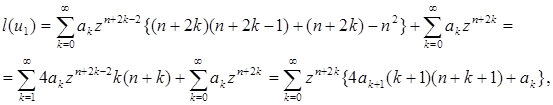
откуда следует так как выражение в фигурных скобках равно нулю. Таким образом, функция удовлетворяет уравнению (1.1), т. е. представляет собой цилиндрическую функцию.

Простейшими функциями рассматриваемого класса являются функции Бесселя порядка нуль и единица:

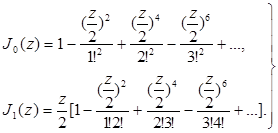(1.3)

Покажем, что функции Бесселя других порядков могут быть выражены через эти две функции. Для доказательства предположим, что а — целое положительное число, умножим ряд (1.2) на и продифференцируем по . Мы получим тогда

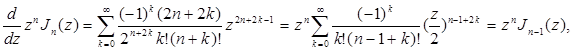
(1.4)

Аналогичным образом, умножая ряд на находим

(1.5)