Курсовая работа: Функции Бесселя

Являясь линейными комбинациями функций и , функции Ханкеля удовлетворяют тем же рекуррентным соотношениям, что и эти функции, например,

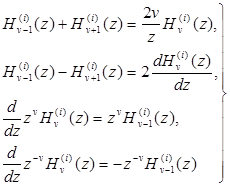(5.3)

и т.д.

Если с помощью (3.5) исключить из (5.1) функцию Бесселя второго рода, то получим

(5.4)

откуда вытекают важные соотношения:

(5.5)

6 Функции Бесселя мнимого аргумента

С функциями Бесселя тесно связаны две часто встречающиеся в приложениях функции и , которые для , принадлежащего плоскости с разрезом вдоль отрицательной полуоси и произвольного , могут быть определены при помощи формул:

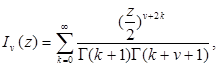
(6.1)

(6.2)

и при целом

(6.3)

Повторяя рассуждения пункта 2, получаем, что и представляют собой регулярные функции в плоскости с разрезом и целые функции .

Рассматриваемые функции просто связаны с функциями Бесселя от аргумента .

Действительно, предположим, что . Тогда и из (2.1) следует

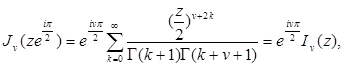
откуда

(6.4)

для всех

Аналогично из формулы (5.4) получаем для таких же

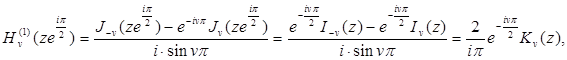
откуда

(6.5)

Для значений функции и могут быть выражены через функции Бесселя от аргумента . Мы имеем

(6.6)

для всех .

На основании полученных соотношений функции и называются функциями Бесселя мнимого аргумента. Функция известна в литературе также под названием функции Макдональда.