Курсовая работа: Функции Бесселя

(1.6)

откуда непосредственно следует:

(1.7)

(1.8)

Полученные формулы известны под названием рекуррентных соотношений для функций Бесселя.

Первое из соотношений дает возможность выразить функцию произвольного порядка через функции порядков нуль и единица, что существенным образом сокращает работу по составлению таблиц функций Бесселя.

Второе соотношение позволяет представить производные от функций Бесселя через функции Бесселя. Для это соотношение должно быть заменено формулой

(1.9)

непосредственно вытекающей из определения данных функций.

Функции Бесселя первого рода просто связаны с коэффициентами разложения функции в ряд Лорана [1]):

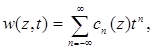
(1.10)

Коэффициенты этого разложения могут быть вычислены путем перемножения степенных рядов:

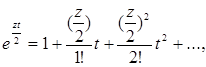
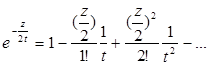
и объединения членов, содержащих одинаковые степени . Выполнив это, получим:

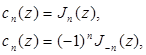
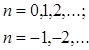(1.11)

откуда следует, что рассматриваемое разложение может быть записано в виде

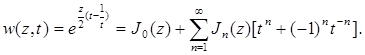(1.12)

Функция называется производящей функцией для функций Бесселя с целым значком; найденное соотношение (1.12) играет важную роль в теории этих функций.

Для получения общего интеграла уравнения (1.1), дающего выражение произвольной цилиндрической функции с целым значком , необходимо построить второе решение уравнения, линейно независимое с . В качестве такого решения может быть взята функция Бесселя второго рода, исходя из определения которой нетрудно получить для аналитическое выражение в виде ряда

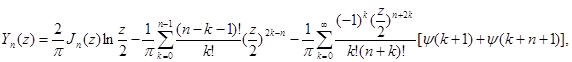(1.13)

где

( – постоянная Эйлера) и, в случае , первую из сумм надлежит положить равной нулю.

Функция регулярна в плоскости с разрезом . Существенная особенность рассматриваемого решения состоит в том, что оно обращается в бесконечность, когда . Общее выражение цилиндрической функции для представляет линейную комбинацию построенных решений

(1.14)

где и – произвольные постоянные,

2 Функции Бесселя с произвольным значком

бессель цилиндрическая функция

Функции Бесселя, рассмотренные в пункте 1, составляют частный случай цилиндрических функций более общего вида, известных под названием функций Бесселя первого рода с произвольным значком . Чтобы определить эти функции, рассмотрим ряд

где – комплексное переменное, принадлежащее плоскости с разрезом