Содержание

1. Введение

2. Постановка задачи

3. Нахождение собственных чисел и построение ФСР

4. Построение фундаментальной матрицы решений методом Эйлера

5. Нахождение приближённого решения в виде матричного ряда

6. Построение общего решения матричным методом

7. Задача Коши для матричного метода

8. Решение неоднородной системы

Графики

Заключение

1. Введение

Рассмотрим систему линейных уравнений первого порядка, записанную в нормальной форме:

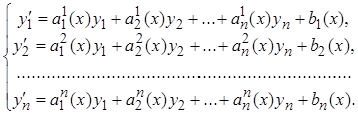(1)

где коэффициенты а_ij , i=1,2,…..,n, к=1,2,…,n, являются постоянными величинами;

y_i =y_i (t), i=1,2,…,n - неизвестные функции переменной t.

Если все b_i (t) (i=1,2,…,n) положить равным нулю (b_i (t)=0), то получится однородная система, соответствующая неоднородной системе (1).

Обозначая матрицу системы через А(х), а вектор через тогда систему (1) можем переписать в матричной форме

(1а)

Если , то получаем соответствующую систему однородных уравнений

. (2)

Всякая совокупность n функций

определенных и непрерывно дифференцируемых в интервале (a;b), называется решением системы (1) в этом интервале, если она обращает все уравнения системы (1) в тождества:

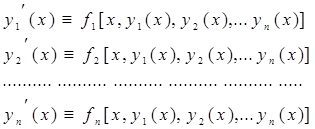
справедливые при всех значениях x из интервала (a, b). Общее решение неоднородной системы представляет собой сумму общего решения соответствующей однородной системы и частного решения неоднородной.

2. Постановка задачи

Цель работы: исследование методов решения системы дифференциальных уравнений с постоянной матрицей:

;;

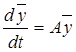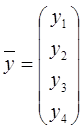
Задание

1. Найти собственные числа и построить фундаментальную систему решений (ФСР).

2. Построить фундаментальную матрицу методом Эйлера.

3. Найти приближенное решение в виде матричного ряда.

4. Построить общее решение матричным методом. Исследовать зависимость Жордановой формы матрицы А от ее собственных чисел.

5. Решить задачу Коши.

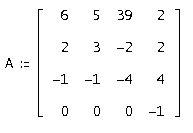
--> ЧИТАТЬ ПОЛНОСТЬЮ <--