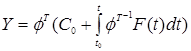Необходимо из всех решений системы уравнений найти такое решение, в котором y^{( i )} (t) принимает заданное числовое значение y_{0 i} в заданной точке, т.е. найти значения с_i для следующих заданных значений: x=0, y=[1, 2, 3,4].

В вектор решений y(t) подставляем заданные условия и решаем полученную систему относительно c1, c2, c3, c4:

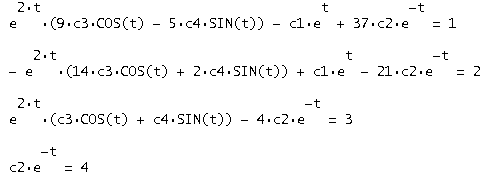
В результате получаем:

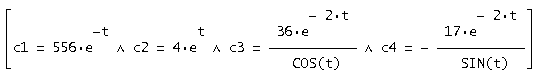
При подстановке c1, c2, c3, c4в общее решение получим решение в форме Коши:

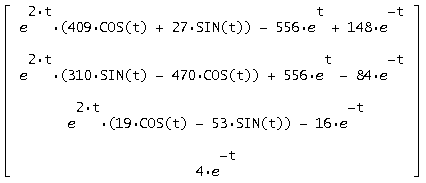
Сделаем проверку, подставив общее решение в исходную систему

:

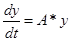Получился нулевой вектор . Следовательно, найденная матрица является решением исходной системы.

Исследование зависимости жордановой формы матрицы А от свойств матрицы системы

Пусть J – жорданова клетка матрицы А. Для случая действительных разных корней жорданова клетка будет выглядеть следующим образом:

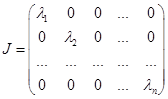
Пусть среди действительных собственных чисел матрицы А есть кратные. Жорданова клетка будет находиться по следующей формуле:

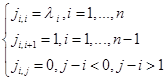
Например, если кратность k=2, то жорданову клетку матрицы мы можем записать так:

Если кратность k=3, то жорданову клетку матрицы мы можем записать так:

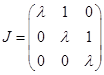
Если же среди трех собственных чисел являются корнями кратности 2, то жорданова форма будет выглядеть следующим образом:

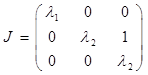
Если два собственных числа матрицы А являются комплексными сопряженными, то запись жордановой клетки будет выглядеть так:

где – действительная, – мнимая часть собственного числа .

8. Решение неоднородной системы

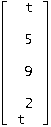
Правая часть:

Общее решение неоднородной системы можно найти по формуле:

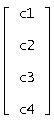Где - фср, Со – матрица , F(t) – вектор правых части.

- общее решение однородной системы

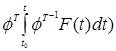- частное решение неоднородной системы

Полученное частное решение неоднородной системы:

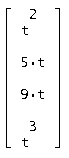
Общее решение однородной системы