Курсовая работа: Исследование методов решения системы дифференциальных уравнений с постоянной матрицей
Тогда их сумма будет искомым общим решением неоднородной системы:
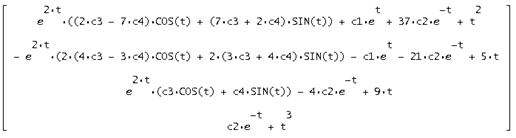
Проверим

Найденное решение верно.
Графики
Изобразим графически точное частное решение однородной линейной системы дифференциальных уравнений с постоянными коэффициентами для начальных условий: t0 = 0, y0 = [1, 2, 3, 4].
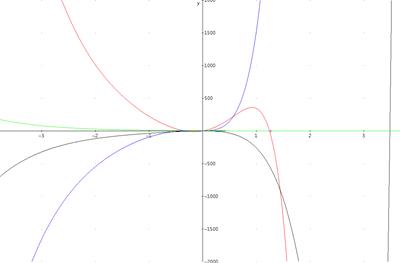
Сравним график одной функции вектора точного решения и одной функции вектора приближенного решения с 3-мя, 5-ю и 7-ю членами ряда:
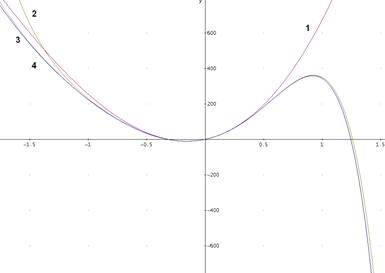
Где 1 – график приближенного решения для трех членов ряда; 2 – график приближенного решения для шести членов ряда; 3 – график приближенного решения для девяти членов ряда; 4 – график точного решения.
Можно сделать вывод:
С увеличением числа членов ряда, число совпадения членов ряда с точным решением будет увеличиваться, область совпадения будет расти.
Заключение
В ходе проделанной работы было изучено 3 метода нахождения общего решения однородной системы линейных дифференциальных уравнений: метод Эйлера, решение в виде матричного ряда и матричный метод. По сравнению с методом Эйлера и матричным методом, метод разложения в матричный ряд прост в реализации, но дает приближенное решение. Также была изучена задача Коши, которая была использована для нахождения частного решения однородной системы линейных дифференциальных уравнений для данного вида начальных условий.
Для установления правильности проведенных вычислений была проведена проверка с помощью подстановки полученных решений в исходную систему уравнений.
Для реализации этой работы в DERIVE были использованы следующие функции пакета:
1. EIGENVALUES (A, ![]() ) – вычисление собственных чисел матрицы A с последующей записью в вектор
) – вычисление собственных чисел матрицы A с последующей записью в вектор ![]() .
.
2. SOLVE (Pm=0, ![]() ) – решение уравнения Pm=0, где Pm – полином степени m: Pm=p0*
) – решение уравнения Pm=0, где Pm – полином степени m: Pm=p0*![]() m p1*
m p1*![]() m -1 +…+pm-1*
m -1 +…+pm-1*![]() +pm, а
+pm, а ![]() - переменная, относительно которой решается данное уравнение.
- переменная, относительно которой решается данное уравнение.
3. EXACT_VECTOR(A, ![]() ) – вычисление точного собственного вектора матрицы А и размещение этих значений в
) – вычисление точного собственного вектора матрицы А и размещение этих значений в ![]() .
.
4. DIF(A,x,n) – дифференцирование A по xn раз.
5. SUM(M,n,f,g) – вычисление суммы M по n изменяющимся с f до g.
6. VECTOR(u,k,n)– задание (вычисление) вектора значений при k изменяющемся от 1 до n.
А также функции меню:
1. SOLVE/SYSTEM –решение системы с последующим заданием в диалоговом окне количества уравнений, самих уравнений и переменных, относительно которых решается данное уравнение.
2. Simplify > Expand– раскрытиевыражений.
Команда Expand используется для раскрытия математических выражений.
Expand expression: #n: где n – номер строки выражения (операнда).
Expand Variable: #n .
В этом варианте команды необходимо указать имя переменной, по которой будет проведено преобразование. Если по всем -<Enter>.