Курсовая работа: Исследование рычажного и зубчатого механизмов

W=3*3-2*4=1

Степень подвижности механизма равна 1, что свидетельствует о наличии только одного входного звена (звено 1). Если этому звену задать движение с некоторой угловой скоростью, то все остальные звенья механизма будут совершать строго определенные движения.

1.1.3 Структурный анализ на уровне групп Ассура

Исходный механизм I (0;1):n=1; р₅ =1

Определить степень подвижности W=3n-2p

W=3*1-2*1=1

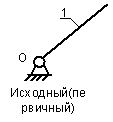
Рисунок 2- Исходный механизм

Вывод: Так как степень подвижности равна 1, следовательно, это исходный механизм.

Группа Ассура второго класса, второго вида II₂ (2;3): n=2; p₅ =3.

Определить степень подвижности W=3n-2p

W=3*2-2*3=0

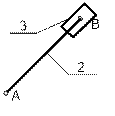
Рисунок 3- Группы Ассура

Вывод: Так как степень подвижности равна 0, следовательно, это группа Асура. Формула механизма: I (0; 1) II₂ (2; 3)

Вывод: Механизм является механизмом второго класса, так как наивысший класс группы Ассура равен II.

1.2 Кинематический анализ механизма (лист 1)

Задачи кинематики:

1. Задача положения состоит в определении функции положения;

2. Задача о скоростях, заключается в отыскании аналогов линейных и угловых скоростей;

3. Задача положения, аналога скорости и аналога ускорения центра масс каждого звена;

4. Задача углового положения, аналогов угловой скорости и углового ускорения звеньев;

5. Определение крайних положений механизма и величины хода выходного звена.

1.2.1 Анализ движения исходного механизма I (0,1)

Рисунок 4-Входное звено

Принимаем угол Ψ = 30^о

Ψ=30^о =0.5235 рад

Cos 30=0.8660 рад