Курсовая работа: Исследование систем автоматического управления (САУ)

Исследуем САУ на астатизм по полученной передаточной функции ошибки:

А) определяем С0:

.

так как С0 = 0, то эта система астатическая;

Б) определяем С1:

так как , то система является астатической первого порядка.

4. Исследование устойчивости исходной замкнутой САУ

4.1 Исследование устойчивости САУ по критерию Гурвица

Критерием, пригодным для оценки устойчивости уравнений порядка выше третьего, является критерий немецкого математика Гурвица. Составим характеристическое уравнение исходной замкнутой САУ:

Обозначим

;

;

;

.

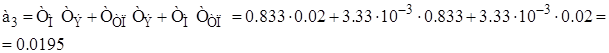
Составим определитель Гурвица по определению:

;

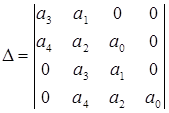Составим диагональные миноры:

;

;

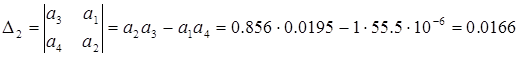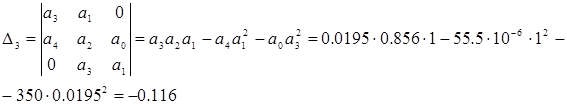
Итак, получаем, что ; ; , т.е. условие устойчивости системы не выполняется, а следовательно система по критерию Гурвица неустойчива.

4.2 Исследование устойчивости САУ по критерию Найквиста

В соответствии со структурной схемой (рис.3) АЧХ и ФЧХ разомкнутой САУ можно представить в виде произведения АЧХ и суммы ФЧХ элементарных динамических звеньев:

а) интегрирующего звена:

, ;