Курсовая работа: Исследование систем автоматического управления (САУ)
![]() ,
,![]() ;
;
в) апериодического звена первого порядка:
![]() ,
,![]() ;
;
г) апериодического звена первого порядка:
![]() ,
,![]() ;
;
Задаемся определенным значением частоты и определяем АЧХ и ФЧХ для каждого звена. Результаты вычислений сведены в табл.2. Причем
A (w) = A1(w)A2(w)A3(w)A4(w);
j(w) = j1(w)+j2(w)+j3(w)+j4(w).
По данным табл.2 строим АФЧХ исходной разомкнутой САУ. Снимая показания, видим, что график при пересечении отрицательной вещественной оси охватывает точку с координатами (-1;j0). Следовательно исходная система неустойчива.
Табл. 2
| Звенья | w,с-1 | |||||||||
| 0 | 2 | 5 | 10 | 20 | 50 | 100 | 150 | 200 | ||
| W1(jw) | A1(w) | ¥ | 175 | 70 | 35 | 17,5 | 7 | 3,5 | 2,3 | 1,75 |
| j1(w) | -90 | -90 | -90 | -90 | -90 | -90 | -90 | -90 | -90 | |
| W2(jw) | A2(w) | 1 | 1 | 0,999 | 0,999 | 0,998 | 0,986 | 0,949 | 0,895 | 0,832 |
| j2(w) | 0 | -0,38 | -0,95 | -1,91 | -3,81 | -9,45 | -18,4 | -26,5 | -33,7 | |
| W3(jw) | A3(w) | 1 | 0,51 | 0,23 | 0,12 | 0,06 | 0,02 | 0,012 | 0,008 | 0,006 |
| j3(w) | 0 | -59 | -76,5 | -83,2 | -86,6 | -88,6 | -89,3 | -89,5 | -89,7 | |
| W4(jw) | A4(w) | 1 | 0,999 | 0,995 | 0,981 | 0,928 | 0,707 | 0,447 | 0,316 | 0,243 |
| j4(w) | 0 | -2,3 | -5,7 | -11,3 | -21,8 | -45 | -63,4 | -71,6 | -76 | |
| A(w) | ¥ | 89,2 | 16 | 4,12 | 0,97 | 0,1 | 0,02 | 0,005 | 0 | |
| j(w) | -90 | -152 | -173 | -186 | -202 | -233 | -261 | -277 | -289 | |
4.3 Исследование устойчивости САУ по логарифмическому критерию
Для исследования САУ по логарифмическому критерию строим логарифмические амплитудно-частотную (ЛАЧХ) и фазочастотную (ЛФЧХ) характеристики разомкнутой САУ. Для этого определяем частоты сопряжения
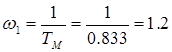 с-1;
с-1;
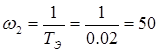 с-1;
с-1;
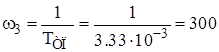 с-1;
с-1;
коэффициент усиления САУ
![]() дб.
дб.
наклон первой асимптоты — -20 дб/дек;
наклон второй изменяется на -20дб/дек и составляет — -40 дб/дек;
наклон третьей изменяется на -20 дб/дек и составляет — -60 дб/дек;
наклон четвёртой изменяется на -20 дб/дек и составляет — -80 дб/дек;
Для построения ЛФЧХ используем данные табл. 2. Из характеристик очевидно, что система неустойчива, так как ЛФЧХ пересекает ось w раньше, чем ЛАЧХ.
4.4 Сопоставление результатов исследования устойчивости различными методами
Рассмотренные выше критерии устойчивости дали один и тот же результат. Однако, с точки зрения практического использования они неравноценны.
Критерий Гурвица позволяет получить только качественное суждение о характере процесса регулирования, т.е. устойчивость, устойчив или нет процесс; но он является наиболее точным. А также данный метод позволяет определить предельный коэффициент усиления САУ.
Частотный критерий Найквиста применяется тогда, когда трудно получить уравнения всех звеньев, но можно получить экспериментально - фазовые их характеристики. Устойчивость по данному методу определяется по тому, как АФЧХ охватывает точку с координатами (-1; j0).
Кроме того, расположение ЛФЧХ еще не дает прямого ответа, устойчива ли система, что требует дополнительных исследований.
При использовании логарифмических частотных характеристик оценка устойчивости системы производится проще, т.е. по их виду можно заключить, устойчива система или нет; но можно получить противоречивые показания, так как мы используем приближенную ЛАЧХ, вместо точной.
5. Синтез последовательного корректирующего устройства