Курсовая работа: Изучение и анализ различных способов определение тригонометрических функций

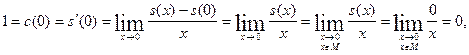
т.е. . Поскольку полученное равенство ложно, то наше допущение об отсутствии наименьшего положительного нуля функции неверно, и тем самым требуемое свойство доказано.

Обозначим наименьший положительный нуль функции через . Выясним свойства функций и , прямо или косвенно связанные с числом ().

6. Функция положительна на интервале и отрицательна на интервале .

7. Функция убывает на и возрастает на .

8. Числа вида и только эти числа являются нулями функции .

Доказательство. Согласно замечанию к лемме 2, (). Если же (), то . Для доказательства этого допустим противное, т.е. предположим, что существует число (), такое что . Без ограничения общности (учитывая нечётность функции ) можем считать, что . Пусть . Положим . Очевидно, что . Кроме того, на основании свойств 2 и 4 получим

т.е. функция имеет нуль в интервале вопреки определению числа .

9. , ; , .

10. Функция положительна на и отрицательна на .

Доказательство.

1) Докажем, что на .

, (по свойству 9). Найдём :

, т.к. , то , следовательно , т.е . Учитывая свойство 7 получим, что - наименьший положительный нуль функции .

Учитывая, что и свойство 7, получаем, что - наибольший отрицательный нуль функции .

Таким образом, но интервале функция не имеет нулей. По теореме Больцано-Коши функция будет знакопостоянной на этом интервале. Кроме того, функция положительна в некоторой правосторонней окрестности точки (в силу того, что (по свойству 9) ). Следовательно, на всём интервале , следовательно, и на .

2) Докажем, что на .

(по свойству 9). Найдём :

, т.к. , то , следовательно , т.е . Учитывая свойство 7 получим, что - наибольший отрицательный нуль функции .

Таким образом, но интервале функция не имеет нулей. По теореме Больцано-Коши функция будет знакопостоянной на этом интервале. Кроме того, функция отрицательна в некоторой правосторонней окрестности точки (в силу того, что , ). Следовательно, на всём интервале .

11. .

Действительно, из равенства имеем , откуда, учитывая, что , получим .

12. Функция возрастает на и убывает на .

Доказательство. Прежде всего, функция непрерывна на каждом из отрезков и и дифференцируема на .

Так как , то учитывая свойство 10, на и на .Требуемое утверждение теперь непосредственно следует из теоремы о достаточных условиях убывания (возрастания) функции на промежутке.

Замечание . Из свойства 2 и 12 следует, что функция убывает на и возрастает на .

13. Функции ,- периодические с периодом .

Доказательство. Применяя теоремы сложения и учитывая, что , , имеем при любом :