Курсовая работа: Изучение и анализ различных способов определение тригонометрических функций

.

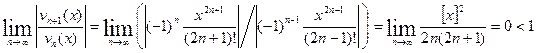Следовательно, функции и как суммы соответствующих степенных рядов (1) и (2) определены и непрерывны на интервале . Более того, эти функции дифференцируемы на , причём

Функция чётная, а нечётная, так как , для любого .

Установим ещё некоторые свойства функций и .

Теорема1. Для любого действительного

. (3)

Доказательство. Имеем

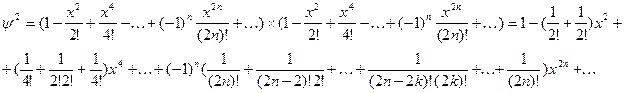
Коэффициент при можно представить в виде

ибо - число сочетаний из элементов по

Аналогично

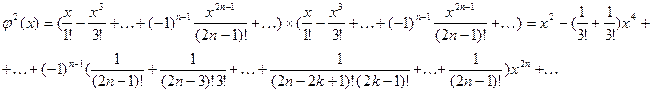
Коэффициент при можно представить в виде

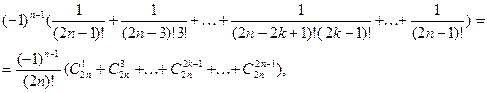
ибо

При сложении и коэффициент при будет равен

Выражение в скобках равно нулю, в чём можно убедиться, полагая , в формуле бинома Ньютона

Таким образом, .

Следствие. Функции и ограниченные, причём и

Теорема 2 . (теорема сложения для функций и ). Для любых действительных и

(4)

(5)

Доказательство . Проверим формулу:

Имеем: