Курсовая работа: Изучение и анализ различных способов определение тригонометрических функций

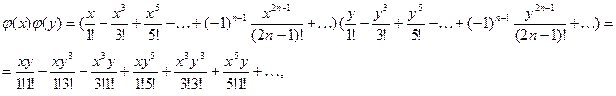
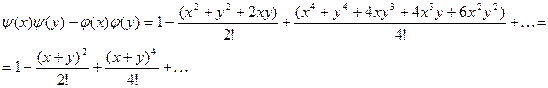
Рассмотрим общий член этого ряда, содержащий произведения вида: , где . Получим

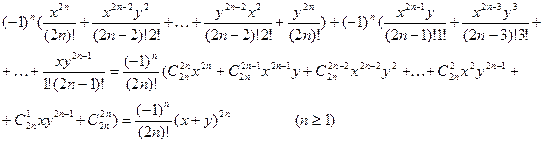
ибо

Таким образом,

.

Используя чётность или нечётность функций и , проверим справедливость формулы:

Имеем

Аналогично проверяется справедливость формул

Теорема3. Для любых действительных и функция удовлетворяет уравнению

(6)

Доказательство. По определению функцииимеем:

Вычислим - общий член ряда для суммы

Далее,

Вычислим - общий член ряда для произведения

ибо Получим, что при , а поскольку , то при любых действительных и имеет место равенство (6).

Замечание1. Из формул сложения (3) и (4) следуют формулы двойного аргумента:

(7)

Замечание2. Непосредственно из формул (3) и (7) получим: