Задание

Теоретическая часть

Метод ветвей и границ

Метод наискорейшего спуска

Практическая часть

Задача №1

Задача №2

Задание

Определение последовательности проведения проверок с использованием метода ветвей и границ, и количества повторных измерений методом наискорейшего спуска при ограничении на время проверок.

Дано:

1. Граф исходного множества модулей и таблицы длительности операций.

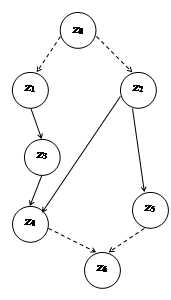
№ вершины	Z1	Z2	Z3	Z4	Z5
Длительность, τi	2	4	5	3	8

Дуги	1-3	2-4	2-5	3-4
Длительность, tij	15	12	3	7

2. Характеристики параметров, допуски и погрешность измерений.

№ параметра	1	2	3	4	5
σИЗМ /σПАР	0.1	0.3	0.5	0.2	0.4
ti	20	30	15	50	5

Теоретическая часть

Метод ветвей и границ

Наиболее перспективным способом решения оптимизационных задач контроля является метод ветвей и границ.

Идея этого метода заключается в следующем. Множество W(S₀ ) всех допустимых вариантов решения σ разбивается на непересекающиеся подмножества W(S_k ), которые, в свою очередь, разбиваются на подмножества меньшей мощности W(S_l ) до получения подмножества W(S_v ), состоящего из единственного варианта. Процесс разбиения множества допустимых вариантов W(S₀ ) на их непересекающиеся подмножества называется ветвлением вариантов, а получаемое при этом дерево – деревом решений. Каждой вершине дерева ветвления соответствует некоторый модуль из графа, а любой путь по дереву определяет соответствующий граф очередности. Множество вершин описывает определенный вариант процесса.

Пусть Y(S_k ) – множество вершин в графе очередности D, соответствующих пути от S₀ до S_к в дереве Е. из каждой вершины S_к выходит столько ветвей, сколько допустимых модулей (претендентов упорядочения) имеется в подмножестве Z\ Y(S_k ). Множество допустимых на каждом шаге процесса ветвления модулей образует фронт упорядочения. Наглядное представление об образовании фронта упорядочения дает преобразованный в соответствии с формулой (1.1) граф G

F(z_l ) = max[f(z_i ) + t_il ] (1.1)

z_i →z_j

Очевидно, на первом шаге процесса построения дерева Е фронт упорядочения образуют вершины, которые соединены с мажорантой одной дугой, на втором шаге к ним добавляются все последователи включенной в D вершины, в которую не входят дуги из других вершин и т.д. На произвольном шаге фронт упорядочения образуют модули, для которых Г₀ ^-1 z_i = Ø.

Метод ветвей и границ предполагает построение дерева ветвления вариантов Е и фактически представляет собой процедуру последовательного анализа вариантов, дополненную прогнозированием такого направления поиска, в котором с наибольшей вероятностью находится оптимальное решение. Идея прогнозирования заключается в оценке нижних границ минимизируемой целевой функции для разветвляемых подмножеств W(S_k ). На каждом шаге ветвление продолжается из вершины, имеющей минимальную оценку. Задача сводится к отысканию на дереве конечной вершины, соответствующей оптимальному допустимому решению со значением целевой функции, меньшим или равным оценкам висячих вершин дерева Е.

Как показывает практика применения метода ветвей и границ, эффективность его значительно зависит от способа представления решения в виде дерева вариантов и метода оценки нижней границы целевой функции.

Для минимизации этот метод может быть применен следующим образом.

На основе исходной информации, заданной графом G, построим

│Z│– размерные матрицы, такие что

τ_i + t_ij , если (i,j) принадлежит U

b_ij = (1.2)

- ∞, если (i,j) не принадлежит U

--> ЧИТАТЬ ПОЛНОСТЬЮ <--