Курсовая работа: Контроль и диагностика систем

При достижении в процессе ветвления подмножества W(S_ν ), состоящего из единственного варианта D(S_ν ) = [Y(S_ν ), Г_D ], Y(S_ν ) = Z, последний будет оптимальным если

t*(S_ν ) ≤ min{ Т_оц (S_k )│ S_k є S*}. (1.12)

если (12) не выполняется, то поиск оптимального решения продолжается из вершины, имеющей наименьшую из оценок Т_оц (S_{k *} ).

Метод наискорейшего спуска

На автоматизированный контроль объектов отводится определенное время, между тем при однократных измерениях выбранного количества контролируемых параметров это время полностью не используется, т.е. остается некоторый избыток времени. Эту избыточность времени можно использовать в целях повышения достоверности результатов автоматизированного контроля сложных объектов применением многократных (повторных) измерений контролируемых параметров. Таким образом, возникает задача оптимального использования временной избыточности или, что то же самое, при контроле совокупности параметров возникает задача определения оптимального количества повторных измерений, обеспечивающего максимальную достоверность результатов контроля.

Рассмотрим задачу:

Требуется обеспечить не менее, чем заданную достоверность результатов контроля при условии, что суммарно время измерения контролируемых параметров не превысит некоторой величины.

Введем следующие обозначения:

Р – достоверность результатов контроля объекта (вероятность получения правильных результатов, Р₀ – заданное значение );

Т – суммарное время измерения всех контролируемых параметров (Т0 – заданное значение);

m – количество контролируемых параметров;

n_i – количество повторных измерений i-го параметра;

t_i – время одного измерения i-го параметра;

p_i (n_i ) – достоверность результатов контроля i-го параметра при n_i – кратном измерении.

Тогда задача формулируется: найти

(2.1)

при условии, что выполняется ограничение

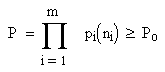(2.2)

контролируемые параметры независимы.

Р^{( N )} – достоверность результатов контроля на N-ом этапе процесса решения;

Т^{( N )} – суммарное время измерения всех контролируемых параметров на N-ом этапе процесса решения.

Сущность метода заключается в следующем. Берется исходный состав контролируемых параметров, которые определяют работоспособность объекта, и для них вычисляются значения достоверности контроля Р⁽¹⁾ и суммарное время измерения этих параметров Т⁽¹⁾ при однократных измерениях (индекс “1” означает отсутствие повторения измерений)

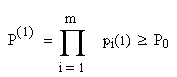(2.3)

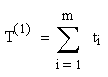(2.4)

вычисляем

ψ_i (n_i ) = (p_i (n_i ) – p_i (n_i - 1)) / (p_i (n_i - 1) t_i ) (2.5)

Затем на первом этапе процесса решения последовательно для всех контролируемых параметров (i = 1, 2, ... , m) вычисляются значения Р_i ⁽²⁾ (вероятность получения правильного результата по всем контролируемым параметрам при условии, что i-й параметр измеряется двукратно) и Т_i ⁽²⁾ (суммарное время измерения всех контролируемых параметров при условии, что i-й параметр измеряется двукратно)

P_i ⁽²⁾ = p₁ (1) p₂ (2) ... p_i-1 (1) pi(2) p_i+1 (1) ... p_m (1) (2.6)

T_i ⁽²⁾ = t₁ + t₂ + ... + t_i-1 + 2t_i + t_i+1 + ... + t_m (2.7)

Далее для всех контролируемых параметров на первом этапе вычисляются значения относительного приращения достоверности результатов, в зависимости от приращения суммарного времени измерения.